动态编程( DP )是一种众所周知的算法技术和数学优化,几十年来一直被用于解决计算机科学中的突破性问题。
DP 用例的一个示例是使用 Floyd-Warshall 全对最短路径算法的具有数百或数千个约束或权重的路线优化。另一个用例是使用 Needleman-Wunsch 或 Smith-Waterman 算法进行基因组序列比对的读取比对。
NVIDIA Hopper GPU 动态编程 X ( DPX )指令加速了基因组学、蛋白质组学和机器人路径规划等领域中使用的一大类动态编程算法。加速这些动态编程算法可以帮助研究人员、科学家和从业人员更快地了解潜在的 DNA 或蛋白质结构以及其他几个领域。
什么是动态编程?
DP 技术最初涉及递归地表达算法,其中较大的问题被分解为更容易解决的子问题。
DP 中常用的一种计算优化是保存子问题的结果,并在问题的后续步骤中使用它们,而不是每次都重新计算解决方案。这一步叫做记忆。 Memoization 有助于避免递归步骤,而是支持使用迭代查找表–基于配方。先前计算的结果存储在查找表中。
许多 DP 问题中的一个关键观察结果是,较大问题的解决方案通常涉及计算先前计算的解的最小值或最大值。更大的问题的解决方案在先前解决方案的最小 – 最大值的一个增量内。
一般来说, DP 技术实现了与暴力算法相同的结果,但显著减少了计算需求和执行时间。
DP 示例:加速 Smith-Waterman 算法
NVIDIA Clara Parabricks 是一套 GPU 加速的基因组分析工具,大量使用 Smith-Waterman 算法,并在 NVIDIA GPU 上运行: A100 、 V100 、 A40 、 A30 、 A10 、 A6000 、 T4 ,以及最新的 H100 。
基因组测序具有广泛的应用价值,例如个性化药物或追踪疾病传播。生物中的每个细胞都使用 DNA (或碱基)中的四个核苷酸序列来编码遗传信息。核苷酸是腺嘌呤、胞嘧啶、鸟嘌呤和胸腺嘧啶,由 A 、 C 、 T 和 G 表示。
像病毒这样的简单生物有 10 – 100K 个碱基的序列,而人类 DNA 由大约 30 亿个碱基对组成。有一些仪器(基于化学或电信号)对基因物质的短片段的碱基进行排序,称为读取。这些读数通常为 100 – 100K 碱基长,这取决于用于收集读数的定序器技术。
基因组序列分析中的一个关键计算步骤是对齐读数,以在一对读数中找到最佳匹配。在第二代测序仪中,这些读取长度可以是 100-400 个碱基对,在第三代测序仪的读取长度可以达到 100K 个碱基。对齐读取是一个重复数千万或数亿次的计算步骤。
在寻找最佳匹配方面存在以下挑战:
- 基因组中自然发生的变异,使一个物种内的生物具有特定的特征
- 测序仪器或潜在化学过程导致的读数错误
一对读取之间的最佳匹配相当于一对字符串之间的近似字符串匹配,其中包含奖励匹配和惩罚差异的步骤。 读取之间的差异可能是不匹配、插入或删除。

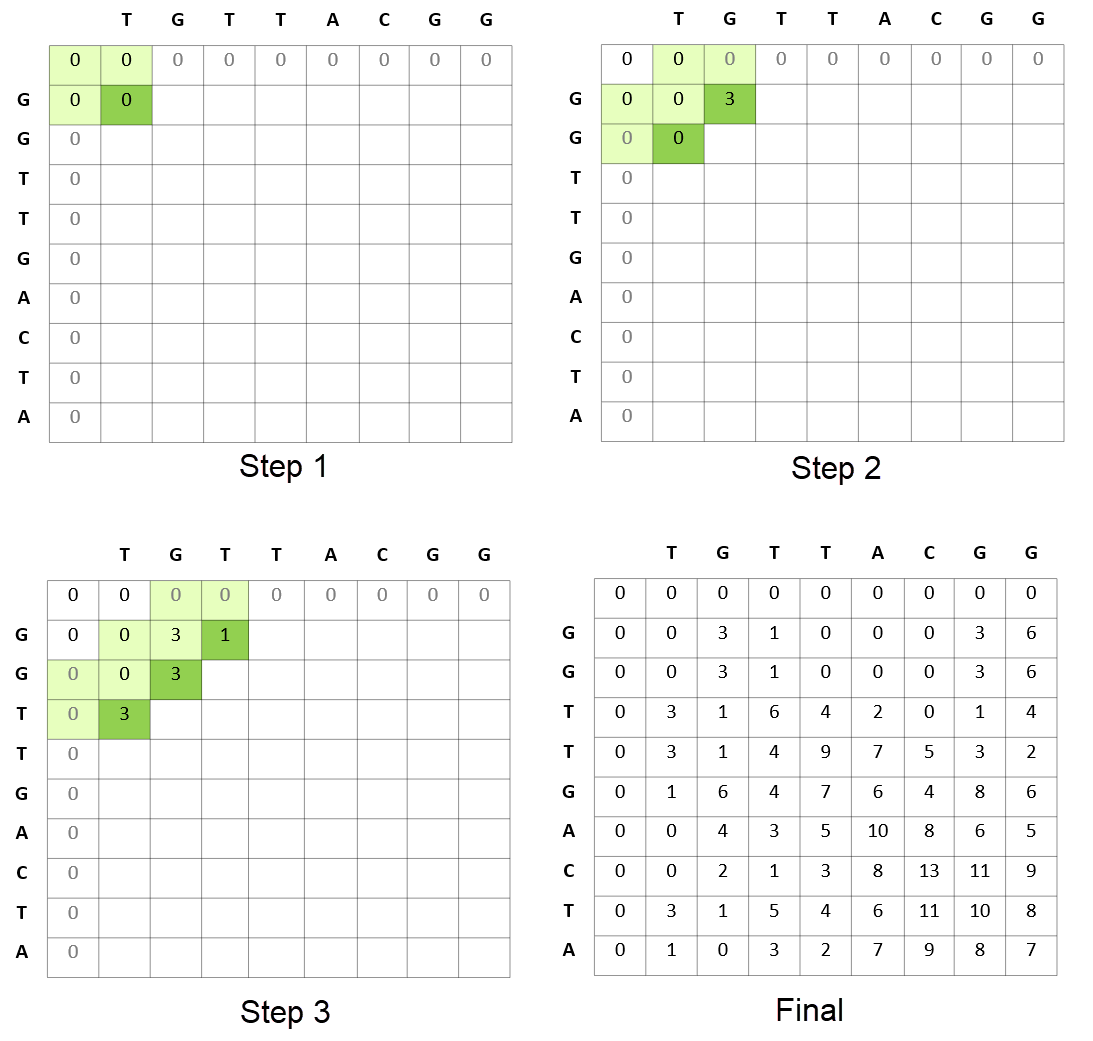
图 1 显示基因组测序中的 Smith-Waterman 步骤旨在找到读取序列 TGTTACGG 和 GGTTGACTA 之间的最佳匹配。所得到的最佳匹配显示为 GTT-AC (来自序列 1 ,“ – ”表示删除)与 GTTGAC (来自于序列 2 )。每个步骤中的得分方案奖励匹配(+ 3 ),惩罚不匹配( -3 ),并惩罚插入和删除(参见图 1 中的差距惩罚公式)。
这是 Smith-Waterman 算法的示例公式。 Smith-Waterman 算法的实现者可以自定义奖励和惩罚。
在计算 TGTTACGG 和 GGTTGACTA 之间的最佳匹配的同时, Smith-Waterman 算法还计算 TGTTAC GG 的所有前缀与 GGTTGATA 的所有前缀的最佳匹配。它从这些序列的开头开始,并使用较小前缀的结果来解决查找较大前缀的解决方案的问题。
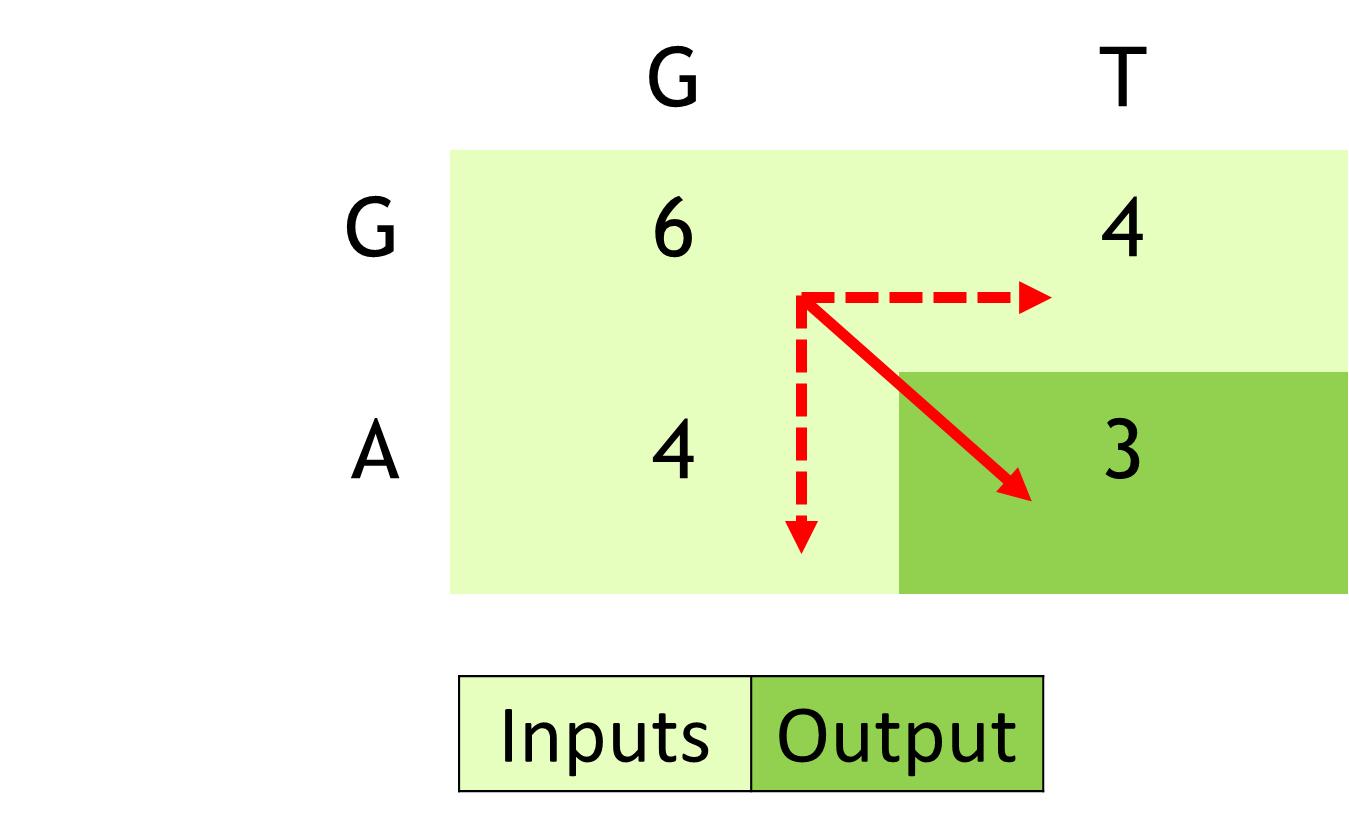
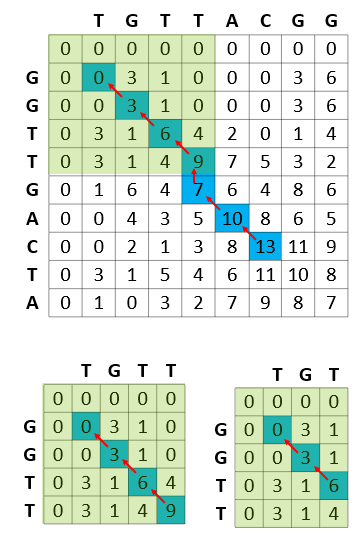
图 3 显示了算法如何计算匹配读取序列的矩阵分数。这种比较匹配是 Smith-Waterman 算法在计算上昂贵的步骤。
这只是 Smith-Waterman 算法如何进行的公式之一。作为示例,不同的公式可以导致算法按行或按列进行。
计算得分矩阵后,下一步包括从最高得分回溯到每个得分的原点。这是一个计算简单的步骤,因为每个单元格都保持其得分的方式(得分计算的源单元格)。
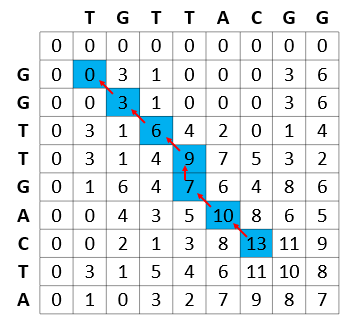
图 5 显示了 Smith-Waterman 计算的计算效率,其中算法所解决的每个子问题都存储在结果矩阵中,并且从不重新计算。
例如,在计算 GGTTGACTA 和 TGTTACGG 的最佳匹配的过程中, Smith-Waterman 算法重用 GGTT ( GGTTGAPTA 的前缀)和 TGTT ( TGTTACGG 的前缀)之间的最佳匹配。反过来,在计算 GGTT 和 TGTT 的最佳匹配时,计算并重用这些字符串的所有前缀的最佳匹配(例如, GGTT 和 TGT 的最佳匹配)。
利用 DPX 指令提高性能
真正的 Smith-Waterman 实现中的内部循环涉及每个单元的以下内容:
- 更新删除惩罚
- 更新插入惩罚
- 基于更新的插入和删除惩罚更新分数。

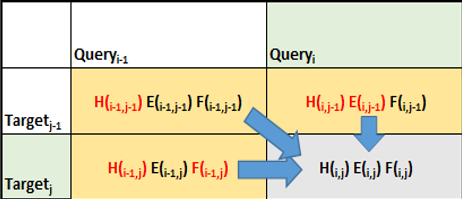
NVIDIA Hopper 架构 math API 为此类计算提供了巨大的加速。 API 将 NVIDIA Hopper 流式多处理器提供的加速作为融合运算(例如,__viaddmin_s16x2_relu,一种按半字执行的内在函数)进行加法运算,然后进行最小或最大加法运算。
Smith-Waterman 软件广泛利用的 API 的另一个示例是三向最小值或最大值,后跟钳位到零(例如__vimax3_s16x2_relu,一种按半字执行的内在值)。
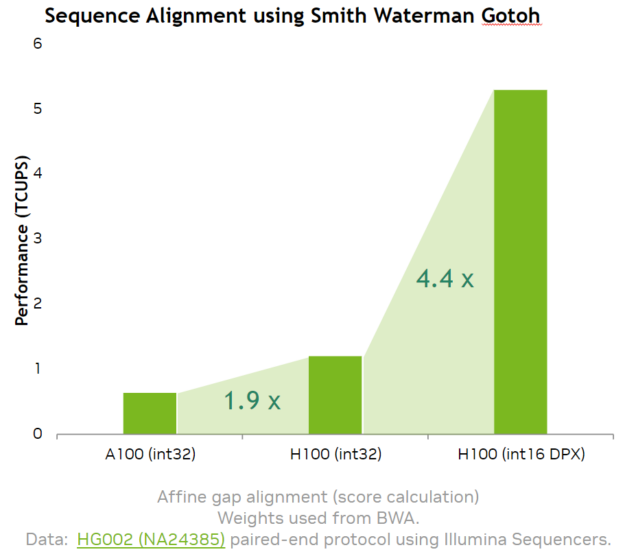
我们使用 NVIDIA Hopper DPX instruction math APIs 实现的 Smith-Waterman 算法的速度比 A100 快 7.8 倍。
Needleman-Wunsch 与部分顺序对齐
与 Smith-Waterman 算法使用 DPX 指令的方式相同,有一大类基本上使用相同原理的对齐算法。
示例包括 Needleman-Wunsch algorithm ,其中算法的基本流程与 Smith-Waterman 非常相似。然而,这两种方法的初始化、插入和间隙惩罚计算不同。
类似 Partial Order Alignment 的算法在其内部循环中密集使用与 Smith-Waterman 单元计算非常相似的单元计算。
所有对最短路径
具有数千或数万个对象的机器人路径规划是仓库中的一个常见问题,仓库中的环境是动态的,有许多移动对象。这些场景可能需要每隔几毫秒进行一次动态重新规划。
大多数全对最短路径算法的内循环如以下 Floyd-Warshall 算法示例所示。伪代码显示了全对最短路径算法如何具有更新每个顶点对之间的最小距离的内循环。最密集的操作基本上是加法运算,然后是最小运算。
initialize(dist); # initialize nearest neighbors to actual distance, all others = infinity
for k in range(V): #order of visiting k values not important, must visit each value
# pick all vertices as source in parallel
Parallel for_each i in range(V):
# Pick all vertices as destinations for the
# above picked source
Parallel for_each j in range(V):
# If vertex k is on the shortest path from
# i to j, then update the value of dist[i][j]
dist[i][j] = min (dist[i][j], dist[i][j] + dist[k][j])
# dist[i][j] calculation can be parallel within each k
# All dist[i][j] for a single ‘k’ must be computed
# before moving to the next ‘k’
Synchronize
DPX 指令所提供的加速功能使其能够以更少的 GPU 和最佳结果来大幅扩展分析对象的数量或实时进行重新优化。
使用 DPX 指令加速动态编程算法
使用 NVIDIA Hopper DPX 指令, Smith-Waterman 在 A100 GPU 上的速度提高了 7.8 倍,这是许多基因组序列比对和变体调用应用中的关键。 CUDA 12 中提供的数学 API 中的公开,使 Smith-Waterman 算法的可配置实现能够满足不同的用户需求,以及 Needleman-Wunsch 等算法。
DPX 指令加速了一大类动态编程算法,如 DNA 或蛋白质测序和机器人路径规划。最重要的是,这些算法可以大大加快疾病诊断、药物发现和机器人自主性,使我们的日常生活变得更好。
致谢
我们要感谢 Bill Dally 、 Alejandro Cachon 、 Mehrzad Samadi 、 Shirish Gadre 、 Daniel Stiffler 、 Rob Van der Wijngaart 、 Joseph Sullivan 、 Nikita Astafev 、 Seamus O ’ Boyle 以及 NVIDIA 的其他许多人。