使用通用稀疏张量建立可扩展的稀疏生态系统

稀疏张量是向量、矩阵以及高维数组在包含大量零元素情况下的推广形式。由于其在存储、计算和功耗方面的高效性，稀疏张量在科学计算、信号处理和深度学习等多个领域中具有重要意义。然而，尽管具备这些优势，通过手工方式或现有库处理稀疏张量通常十分繁琐、容易出错、缺乏可移植性，并且难以应对稀疏模式、数据类型、运算方式及目标平台组合带来的爆炸性增长，导致可扩展性受限。

研究主要侧重于稀疏存储格式，即采用紧凑方式存储非零元素的数据结构，并支持高效的运算，以避免 x = 0 = x 和 x = 0 = 0 等冗余操作。这有助于扩展至更大规模的问题，或在相同规模下以更少的资源完成求解。不存在适用于所有场景的稀疏格式；合适的选择取决于非零元素的分布特征、具体运算类型以及目标架构。

通用稀疏张量 (UST) 将张量的稀疏性与其内存存储表示解耦。UST 采用领域特定语言 (DSL) 来描述张量在内存中的表示方式，使开发者能够专注于张量的稀疏结构。在与稀疏性无关的多态运算中，系统通过编译时或运行时检查操作数所采用的格式，决定将其分派至优化的手写库，或在缺乏相应方案时自动生成稀疏代码。UST 源于稀疏编译器技术，相关研究可参见稀疏矩阵计算编译器支持，稀疏张量代数编译以及MLIR 中稀疏张量计算编译器支持。

本文重点介绍开发者如何利用 UST 定义常见但较为特殊的稀疏存储格式，每种格式均针对其应用中稀疏张量的特定属性进行定制。例如，SciPy、CuPy 和 PyTorch 稀疏张量的可操作性已将 COO、CSR 和 DIA 等常见格式映射到 UST 对应的 DSL 中。此外，开发者还可通过 DSL 定义自身所需的新型稀疏格式。结合调度或代码生成技术，这种方法使得设计新的稀疏格式成为可能，而无需进行显式编码，相关内容将在后续文章中进一步展示。

张量格式 DSL

张量格式 DSL 使用可逆函数来定义每个级别应如何存储，将张量维度（逻辑张量索引）映射到存储级别（物理内存索引）。它包括：

1. 有序的维度规格序列，例如 (i, j)，每个序列均包含一个维度表达式，用于提供各维度的命名引用。

2. 有序的级别规范序列（例如 (i : dense, j : compressed)），每个序列均包含一个级别表达式（用于定义各级别中存储的内容）和一个所需的级别类型（用于定义级别的存储方式），具体包括：

• 级别属性的集合，例如唯一属性和有序属性。
• 所需的关卡格式，例如：
  • dense：表示底层存储仅通过类似密集数组的索引进行
  • compressed：表示在该级别中，位置数组定义存储位置，坐标数组用于存储每个存储级别内的索引
  • singleton：一种压缩形式，其中每个坐标直接隶属于上一级的父坐标
  • range：一种密集形式，其中坐标值基于前一级别的压缩结果

位置和坐标数组以锯齿状（可变大小）数组形式存储，首先按层级（即 pos[l]）索引，再按内容索引，其中位置依照惯例使用两个连续元素定义从 pos[l][i] 到 pos[l][i+1] 的半开区间。若未使用，锯齿状数组将保持为空。在所有层级的末尾，单个数值数组包含所有已存储元素的线性序列。UST 的通用性体现在：上述 DSL 可轻松扩展，以支持更多存储格式。

UST 示例

本节中的 UST 示例表明，随着维度的增加，存储密集和稀疏张量的不同方式的可能性迅速增多。

标量

标量是一个 0 维 (0D) 张量，因此没有维度，也没有层次。因此，UST 存储中的值数组由一个包含标量值的“密集”元素组成 (图 1)。

() -> ()    # scalar

向量

向量是一维（1D）张量，可直观地表示为行向量或列向量。图 2 展示了样本的稀疏行向量。

存储密集向量或压缩向量的两种常见方法如下所示：

(i) -> (i : dense)         # dense vector
(i) -> (i : compressed)    # sparse vector

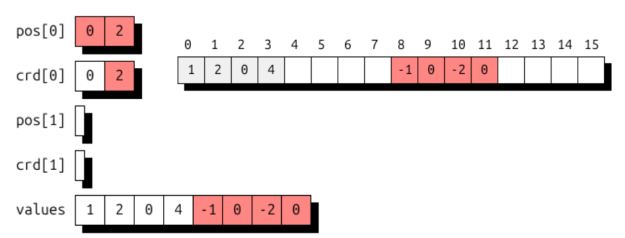
图 3 显示了使用这两种格式的样本向量的 UST 存储。密集存储通过零填充来获取值数组中的填充层级，位置数组和坐标数组均未使用。稀疏存储则利用位置数组定义半开区间 [0, 5)，其中包含每个元素的坐标及其对应的值。

还可以将单个维度映射到两个级别，从而实现块向量存储。下方展示了一个块大小为 4 的示例，该示例本质上是将一个名为 i 的一维空间映射到一个二维空间 (i/4,i%4)。

(i) -> (i / 4 : compressed, i % 4 : dense)    # blocked vector

图 4 显示了样本向量的 UST 存储。通过零填充获得已填充的块。第一级中的位置数组采用【02) 表示两个密集块，第二级数组未被使用。如红色所示，索引为 8 且值为 -1 的元素将映射到块间索引级别 2 和块内索引级别 0。

矩阵

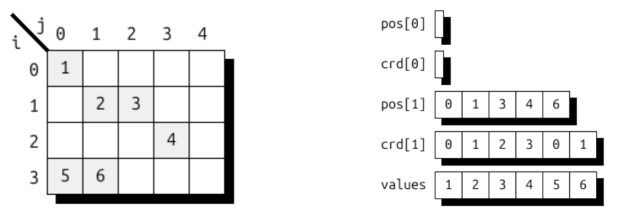
稀疏矩阵存储 (2D) 已经过广泛研究，并且存在许多广泛采用的稀疏存储格式，每种格式都有其独特的名称。UST 的灵活性能够涵盖其中的多数格式，从而将多种变体统一在一个框架之下。

如果仅将密集/压缩的关卡格式与索引排列组合相结合，则 d 维张量的张量格式 DSL 已能生成 2^d✕d！种不同的组合。当 d = 2 时，这将对应八种不同的矩阵格式。

(i, j) -> (i : dense, j : dense)              # Dense (row-major)
(i, j) -> (j : dense, i : dense)              # Dense (col-major)
(i, j) -> (i : dense, j : compressed)         # CSR
(i, j) -> (j : dense, i : compressed)         # CSC
(i, j) -> (i : compressed, j : compressed)    # DCSR
(i, j) -> (j : compressed, i : compressed)    # DCSC
(i, j) -> (i : compressed, j : row)           # CROW (less common)
(i, j) -> (j : compressed, i : row)           # CCOL (less common)

使用行优先或列优先顺序的密集存储非常简单。图 5 展示了具有六个非零元素的 4 × 5 样本矩阵在 CSR 格式下的存储方式。由于第 0 级是密集存储，因此未使用数组 pos[0] 和 crd[0]。相反，i-索引被用作第 1 级的索引，以查找对应行的压缩存储。

在这里，两个连续的位置 pos[1][i] 和 pos[1][i+1] 定义了坐标数组中的半开放位置区间，用于重建每个存储值的 j-index。（采用这种简洁的编码方式时，pos 数组的大小必须始终比实际尺寸多 1。）作为最后一层，实际数值可在 values 数组的相同位置找到。

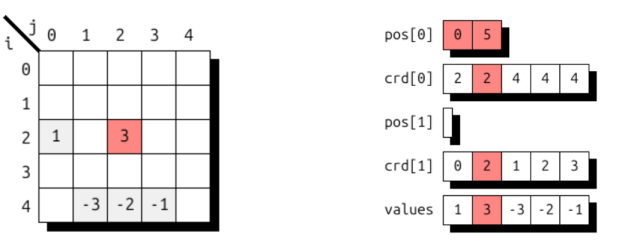
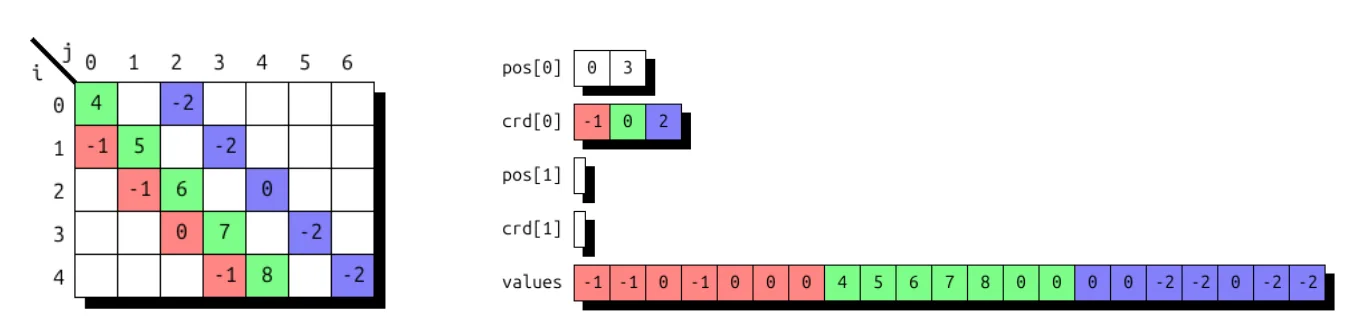
从其他关卡类型来看，COO 格式采用如下所示的 DSL 表示。其中，压缩级别通过非唯一属性来体现，同一索引可多次出现。第二个级别则采用单例级别格式，无需位置数组，因为每个索引都与其父索引直接关联。

(i, j) -> (i : compressed(nonunique), j : singleton)    # COO

在 COO 中存储图 6 中的超稀疏矩阵会生成给定的 UST 格式。着色用于表示元素 a ₂₂ = 3 的存储关系。与之前的格式类似，UST COO 格式在结构上与文献中常见的 COO 格式一一对应，仅在定义存储元素数量的初始位置数组方面存在差异。

范围级别格式可与包含加/子的级别表达式结合，用于定义元素的对角线及反对角线存储。在此，可通过选择行索引或列索引来实现实际存储的密集对角线，从而形成四种变体。

(i, j) -> (j-i : compressed, i : range)    # DIA-I
(i, j) -> (j-i : compressed, j : range)    # DIA-J
(i, j) -> (i+j : compressed, i : range)    # ANTI-DIA-I
(i, j) -> (i+j : compressed, j : range)    # ANTI-DIA-J

对于非方形矩阵，仅使用行索引或列索引之间的差异会变得更加显著。图7中的5×7矩阵样本在图8和图9中分别展示了DIA-I和DIA-J格式。通过着色方式，将存储的对角线与矩阵的对角线进行关联。该格式在范围内外采用零填充以实现完全填充的水平（与内部填充不同，外部填充不对应于原始矩阵索引空间中的元素）。其中，内部和外部填充用于达到完全填充的层次（其中，不像内部填充，外部填充不对应于原始矩阵索引空间中的元素）。）

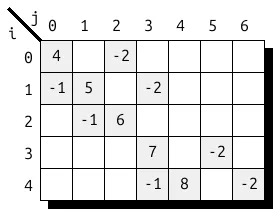
图 8 显示了 DIA-I 格式。

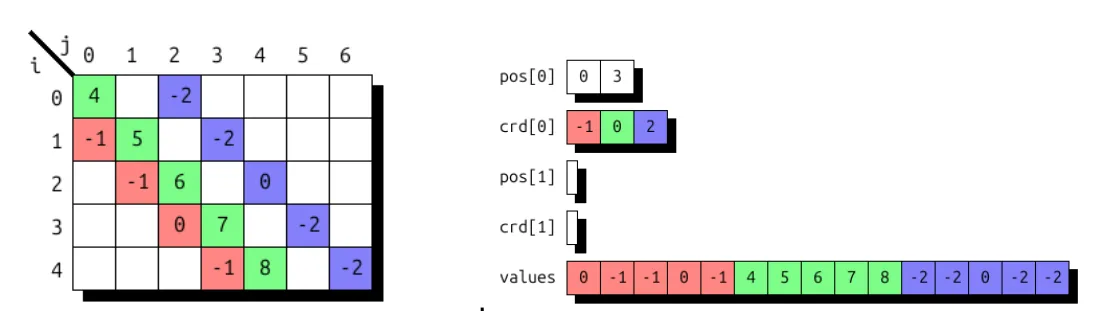
图 9 是相同矩阵的 DIA-J 格式。由于选择较大尺寸的索引会带来更多的零填充，因此在此情况下，优先选用 DIA-I 格式。

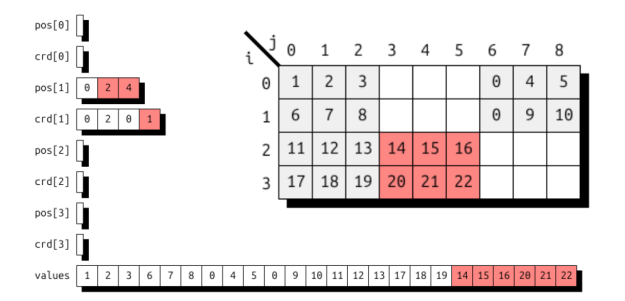
通过分块可以获得更多的存储变体，其中 2D 索引可映射到 3D 级别（成片）或 4D 级别（成块）。对于后者，尽管文献通常仅用 BSR 和 BSC 来定义块之间的行优先或列优先顺序，但 UST 的张量格式 DSL 还能更精确地区分每个存储块内部的行优先和列优先格式，因此对于 2 × 3 块，可产生以下四种变体。

(i, j) -> (i / 2 : compressed, j / 3 : dense,
           i % 2 : dense,      j % 3 : dense)     # BSR-Row(2,3)
(i, j) -> (i / 2 : compressed, j / 3 : dense,
           j % 3 : dense,      i % 2 : dense)     # BSR-Col(2,3)
(i, j) -> (j / 3 : compressed, i / 2 : dense,
           i % 2 : dense,      j % 3 : dense)     # BSC-Row(2,3)
(i, j) -> (j / 3 : compressed, i / 2 : dense,
           j % 3 : dense,      i % 2 : dense)     # BSC-Col(2,3)

图 10 中的 4 × 9 矩阵用于说明块存储。块 B ₁₁ 以其实际所在位置用红色突出显示。例如，可找到一个 ₂₅ = 16 的条目，将维度索引 (25) 映射到水平索引 (1，1，0，2)：块 B ₁₁ 的索引为 (02)。由于该块在压缩行中按主要顺序存储，位于 B ₀₀、B ₀₂ 和 B ₁₀ 之后，成为第四个存储块，而块内按密集行主要顺序存储，使其成为第三个条目，因此最终对应于值数组索引为 20 的元素。

这些示例应能帮助您理解张量格式 DSL 在描述稀疏矩阵存储格式时的表达能力。接下来的章节将探讨更高维度的情况。

张量

如前文所述，仅通过密集/压缩级别类型与 UST 张量格式 DSL 中的索引排列，便可生成 2^d×d！种存储张量的不同方式。当 d = 3、d = 4、d = 5 和 d = 6 时，分别会产生 48、384、3,840 和 46,080 种组合，数量庞大，难以在此一一列出。引入其他层级类型将进一步增加该数值。

举几个存储 3D 张量的例子：UST 的维度排列支持以六种不同的直接方式存储 3D 密集张量，从经典的行主张量到列主张量，以及介于两者之间的各种旋转张量。对所有层级的张量进行压缩存储后，便形成了 CSF（压缩稀疏光纤）格式。

(i, j, k) -> (i : compressed, j : compressed, k : compressed)  # CSF

以图 11 中的 3D 4x3x5 张量为例，该张量在纸上通过依次展示 i=0、i=1、i=2（空）和 i=3 时对应的底层 2D 3 × 5 矩阵来呈现。

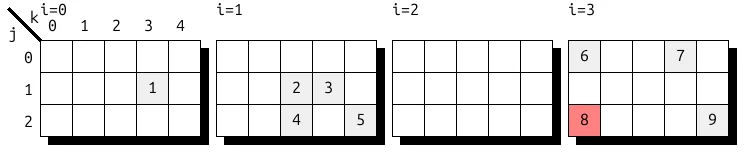
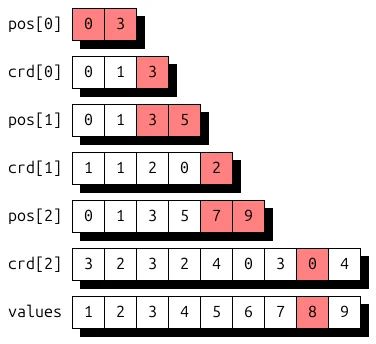
使用 CSF 格式将此张量表示为 UST，将得到如图 12 所示的存储结构。着色部分展示了如何定位存储元素 a₃₂₀ = 8。该格式适用于高度稀疏且非零元素在各维度上分布较为均匀的张量。

3D 张量可视为一组矩阵的批量，这是深度学习中的一个重要概念。将批量维度置于不同位置时，有时会对批量内数据的稀疏均匀性产生有趣的影响。以图 13 中的 3D 4x5x5 张量为例，该张量以 4 个 5 × 5 矩阵的批量形式呈现。

鉴于矩阵内的对角线性质，将此张量存储为批量 DIA 格式是合理的。较为自然的方式是将批量维度变量 i 保留为最外层的密集层级，随后存储矩阵的对角线元素。

(i, j, k) -> (i : dense, k-j : compressed, j : range) # batched DIA-I

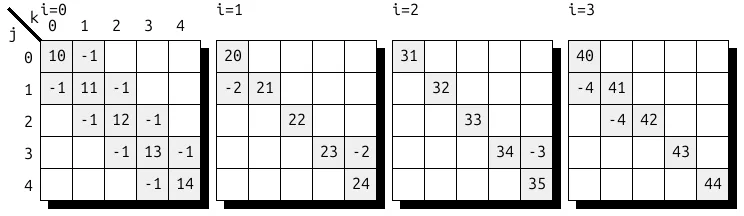
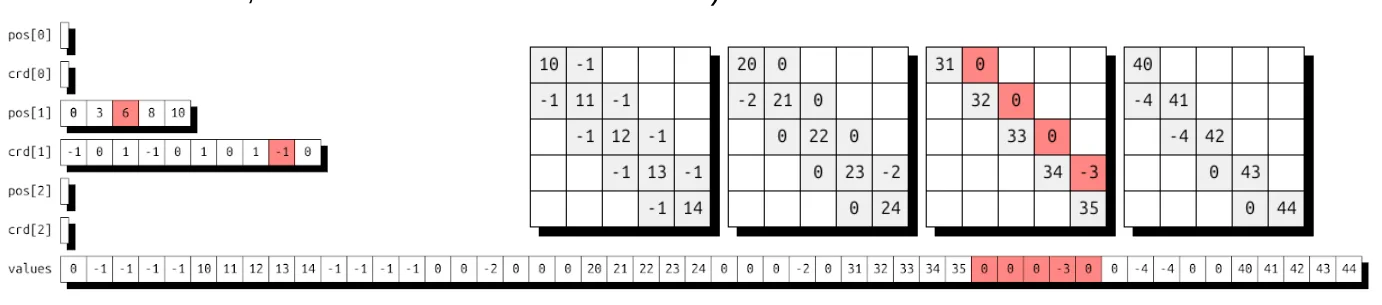
图 14 展示了这种非均匀批量 DIAG-I 存储方式，其中每个批量可具有独立的对角线结构。颜色用于将特定的对角线与其存储位置相对应。为实现完全填充的密集布局，在存储的对角线内部和外部均会进行零填充。坐标数组表示各对角线所在的位置（例如，第一个矩阵位于 -1、0、+1，最后一个矩阵位于 -1 和 0）。

通过将批量变量移至对角线计算的下方，可对张量格式 DSL 进行细微调整：

(i, j, k) -> (k-j : compressed, i : dense, j : range)  # uniform
                                                       # batched CSR

现在，对角线的元数据仅存储一次，但代价是在批处理中的所有矩阵上强制采用统一的对角线非零模式，这可能导致需要额外的零填充，如图 15 所示。

了解详情

本文介绍了 UST 所涵盖的张量存储格式的广泛性。请持续关注 UST 与多态运算的集成，这些多态运算可调度至优化库或自动生成的代码。该方法构建了一个简洁、易用且可扩展的稀疏生态系统，有助于引入无需显式编码的新型存储方案。

想要了解更多信息？立即注册参加 NVIDIA GTC 2026 会议，使用 nvmath-python 加速 GPU 科学计算，观看关于 UST 的精彩演示以及令人期待的产品更新。