
GPU Gems 2
GPU Gems 2 is now available, right here, online. You can purchase a beautifully printed version of this book, and others in the series, at a 30% discount courtesy of InformIT and Addison-Wesley.
The CD content, including demos and content, is available on the web and for download.
Chapter 6. Hardware Occlusion Queries Made Useful
Michael Wimmer
Vienna University of Technology
Jirí Bittner
Vienna University of Technology
6.1 Introduction
Hardware occlusion queries were one of the most eagerly awaited graphics hardware features in a long time. This feature makes it possible for an application to ask the 3D API (OpenGL or Direct3D) whether or not any pixels would be drawn if a particular object were rendered. With this feature, applications can check whether or not the bounding boxes of complex objects are visible; if the bounds are occluded, the application can skip drawing those objects. Hardware occlusion queries are appealing to today's games because they work in completely dynamic scenes.
However, although this feature has been available for more than two years (via the NV/ARB_occlusion_query OpenGL extension and by the IDirect3DQuery9 interface in Direct3D), there is not yet widespread adoption of this feature for solving visibility culling in rendering engines. This is due to two main problems related to naive usage of the occlusion query feature: the overhead caused by issuing the occlusion queries themselves (since each query adds an additional draw call), and the latency caused by waiting for the query results.
In this chapter, we present a simple but powerful algorithm that solves these problems (Bittner et al. 2004): it minimizes the number of issued queries and reduces the impact of delays due to the latency of query results.
To achieve this, the algorithm exploits the spatial and temporal coherence of visibility by reusing the results of occlusion queries from the previous frame in order to initiate and schedule the queries in the current frame. This is done by storing the scene in a hierarchical data structure (such as a k-d tree or octree [Cohen-Or et al. 2003]), processing nodes of the hierarchy in a front-to-back order, and interleaving occlusion queries with the rendering of certain previously visible nodes.
The algorithm is smart about the queries it actually needs to issue: most visible interior nodes of the spatial hierarchy and many small invisible nodes are not tested at all. Furthermore, previously visible nodes are rendered immediately without waiting for their query result, which allows filling the time needed to wait for query results with useful work.
6.2 For Which Scenes Are Occlusion Queries Effective?
Let's recap briefly for which scenes and situations the algorithm presented in this chapter is useful.
Occlusion queries work best for large scenes where only a small portion of the scene is visible each frame—for example, a walkthrough in a city. More generally, the algorithm presented here works if in each frame there are large occluded interior nodes in the hierarchy. These nodes should contain many objects, so that skipping them if they are occluded saves geometry, overdraw, and draw calls (which are a typical bottleneck in today's rendering systems [Wloka 2003]). An important advantage the algorithm has over most other techniques used nowadays in games (such as portal culling) is that it allows completely dynamic environments.
Some games—for example, shader-heavy ones—use a separate initial rendering pass that writes only to the depth buffer. Subsequent passes test against this depth buffer, and thus expensive shading is done only for visible pixels. If the scenes are complex, our occlusion-culling algorithm can be used to accelerate establishing the initial depth buffer and at the same time to obtain a complete visibility classification of the hierarchy. For the subsequent passes, we skip over objects or whole groups of objects that are completely invisible at virtually no cost.
Finally, if there is little or no occlusion in a scene—for example, a flyover of a city—there is no benefit to occlusion culling. Indeed, occlusion queries potentially introduce an overhead in these scenes and make rendering slower, no matter how the occlusion queries are used. If an application uses several modes of navigation, it will pay to switch off occlusion culling for modes in which there is no or only very little occlusion.
6.3 What Is Occlusion Culling?
The term occlusion culling refers to a method that tries to reduce the rendering load on the graphics system by eliminating (that is, culling) objects from the rendering pipeline if they are hidden (that is, occluded) by other objects. There are several methods for doing this.
One way to do occlusion culling is as a preprocess: for any viewpoint (or regions of viewpoints), compute ahead of time what is and is not visible. This technique relies on most of the scene to be static (so visibility relationships do not change) and is thus not applicable for many interactive and dynamic applications (Cohen-Or et al. 2003).
Portal culling is a special case of occlusion culling; a scene is divided into cells (typically rooms) connected via portals (typically door and window openings). This structure is used to find which cells (and objects) are visible from which viewpoint—either in a preprocess or on the fly (Cohen-Or et al. 2003). Like general preprocess occlusion culling, it relies on a largely static scene description, and the room metaphor restricts it to mostly indoor environments.
Online occlusion culling is more general in that it works for fully dynamic scenes. Typical online occlusion-culling techniques work in image space to reduce computation overhead. Even then, however, CPUs are less efficient than, say, GPUs for performing rasterization, and thus CPU-based online occlusion techniques are typically expensive (Cohen-Or et al. 2003).
Fortunately, graphics hardware is very good at rasterization. Recently, an OpenGL extension called NV_occlusion_query, or now ARB_occlusion_query, and Direct3D's occlusion query (D3DQUERYTYPE_OCCLUSION) allow us to query the number of rasterized fragments for any sequence of rendering commands. Testing a single complex object for occlusion works like this (see also Sekulic 2004):
- Initiate an occlusion query.
- Turn off writing to the frame and depth buffer, and disable any superfluous state. Modern graphics hardware is thus able to rasterize at a much higher speed (NVIDIA 2004).
- Render a simple but conservative approximation of the complex object—usually a bounding box: the GPU counts the number of fragments that would actually have passed the depth test.
- Terminate the occlusion query.
- Ask for the result of the query (that is, the number of visible pixels of the approximate geometry).
- If the number of pixels drawn is greater than some threshold (typically zero), render the complex object.
The approximation used in step 3 should be simple so as to speed up the rendering process, but it must cover at least as much screen-space area as the original object, so that the occlusion query does not erroneously classify an object as invisible when it actually is visible. The approximation should thus be much faster to render, and does not modify the frame buffer in any way.
This method works well if the tested object is really complex, but step 5 involves waiting until the result of the query actually becomes available. Since, for example, Direct3D allows a graphics driver to buffer up to three frames of rendering commands, waiting for a query results in potentially large delays. In the rest of this chapter, we refer to steps 1 through 4 as "issuing an occlusion query for an object."
If correctness of the rendered images is not important, a simple way to avoid the delays is to check for the results of the queries only in the following frame (Sekulic 2004). This obviously leads to visible objects being omitted from rendering, which we avoid in this chapter.
6.4 Hierarchical Stop-and-Wait Method
As a first attempt to use occlusion queries, we show a naive occlusion-culling algorithm and extend it to use a hierarchy. In the following section, we show our coherent hierarchical culling algorithm, which makes use of coherence and other tricks to be much more effective than the naive approach.
6.4.1 The Naive Algorithm, or Why Use Hierarchies at All?
To understand why we want to use a hierarchical algorithm, let's take a look at the naive occlusion query algorithm first:
- Sort objects front to back.
- For each object
- Issue occlusion query for the object (steps 1–4 from previous section).
- Stop and wait for result of query.
- If number of visible pixels is greater than 0, render the object.
Although this algorithm calculates correct occlusion information for all of our objects, it is most likely slower than just rendering all the objects directly. The reason is that we have to issue a query and wait for its result for every object in the scene!
Now imagine, for example, a walkthrough of a city scene: We typically see a few hundred objects on screen (buildings, streetlights, cars, and more). But there might be tens of thousands of objects in the scene, most of which are hidden by nearby buildings. If each of these objects is not very complex, then issuing and waiting for queries for all of them is more expensive than just rendering them.
6.4.2 Hierarchies to the Rescue!
We need a mechanism to group objects close to one another so we can treat them as a single object for the occlusion query. That's just what a spatial hierarchy does. Examples of spatial hierarchies are k-d trees, BSP trees, and even standard bounding-volume hierarchies. They all have in common that they partition the scene recursively until the cells of the partition are "small" enough according to some criterion. The result is a tree structure with interior nodes that group other nodes, and leaf nodes that contain actual geometry.
The big advantage of using hierarchies for occlusion queries is that we can now test interior nodes, which contain much more geometry than the individual objects. In our city example, hundreds or even thousands of objects might be grouped into one individual node. If we issue an occlusion query for this node, we save the tests of all of these objects—a potentially huge gain!
If geometry is not the main rendering bottleneck, but rather the number of draw calls issued (Wloka 2003), then making additional draw calls to issue the occlusion queries is a performance loss. With hierarchies, though, interior nodes group a larger number of draw calls, which are all saved if the node is occluded using a single query. So we see that in some cases, a hierarchy is what makes it possible to gain anything at all by using occlusion queries.
6.4.3 Hierarchical Algorithm
The naive hierarchical occlusion-culling algorithm works like this—it is specified for a node within the hierarchy and initially called for the root node:
- Issue occlusion query for the node.
- Stop and wait for the result of the query.
- If the node is visible:
- If it is an interior node:
- Sort the children in front-to-back order.
- Call the algorithm recursively for all children.
- If it is a leaf node, render the objects contained in the node.
- If it is an interior node:
This algorithm can potentially be much faster than the basic naive algorithm, but it has two significant drawbacks.
6.4.4 Problem 1: Stalls
This approach shares the first drawback with the naive algorithm. Whenever we issue an occlusion query for a node, we cannot continue our algorithm until we know the result. But waiting until the query result becomes available may be prohibitive. The query has to be sent to the GPU. There it sits in a command queue until all previous rendering commands have been issued (and modern GPUs can queue up more than one frame's worth of rendering commands!). Then the bounding box associated with the query must be rasterized, and finally the result of the query has to travel back over the bus to the driver.
During all this time, the CPU sits idle, and we have caused a CPU stall. But that's not all. While the CPU sits idle, it doesn't feed the GPU any new rendering commands. Now when the result of the occlusion query arrives, and the CPU has finally figured out what to draw and which commands to feed the GPU next, the command buffer of the GPU has emptied and it has become idle for some time as well. We call this GPU starvation. Obviously, we are not making good use of our resources. Figure 6-1 sums up these problems.
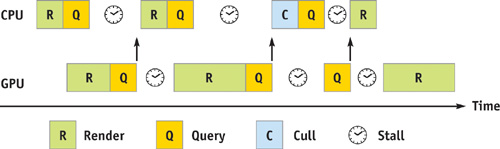
Figure 6-1 CPU Stalls and GPU Starvation Caused by Occlusion Queries
6.4.5 Problem 2: Query Overhead
The second drawback of this algorithm runs contrary to the original intent of the hierarchical method. We wanted to reduce the overhead for the occlusion queries by grouping objects together. Unfortunately, this approach increases the number of queries (especially if many objects are visible): in addition to the queries for the original objects, we have to add queries for their groupings. So we have improved the good case (many objects are occluded), but the bad case (many objects are visible) is even slower than before.
The number of queries is not the only problem. The new queries are for interior nodes of the hierarchy, many of which, especially the root node and its children, will have bounding boxes covering almost the entire screen. In all likelihood, they are also visible. In the worst case, we might end up filling the entire screen tens of times just for rasterizing the bounding geometry of interior nodes.
6.5 Coherent Hierarchical Culling
As we have seen, the hierarchical stop-and-wait method does not make good use of occlusion queries. Let us try to improve on this algorithm now.
6.5.1 Idea 1: Being Smart and Guessing
To solve problem 1, we have to find a way to avoid the latency of the occlusion queries. Let's assume that we could "guess" the outcome of a query. We could then react to our guess instead of the actual result, meaning we don't have to wait for the result, eliminating CPU stalls and GPU starvations.
Now where does our guess come from? The answer lies, as it so often does in computer graphics, in temporal coherence. This is just another way of expressing the fact that in real-time graphics, things don't move around too much from one frame to the next. For our occlusion-culling algorithm, this means that if we know what's visible and what's occluded in one frame, it is very likely that the same classification will be correct for most objects in the following frame as well. So our "guess" is simply the classification from the previous frame.
But wait—there are two ways in which our guess can go wrong: If we assume the node to be visible and it's actually occluded, we will have processed the node needlessly. This can cost some time, but the image will be correct. However, if we guess that a node is occluded and in reality it isn't, we won't process it and some objects will be missing from the image—something we need to avoid!
So if we want to have correct images, we need to verify our guess and rectify our choice in case it was wrong. In the first case (the node was actually occluded), we update the classification for the next frame. In the second case (the node was actually visible), we just process (that is, traverse or render) the node normally. The good news is that we can do all of this later, whenever the query result arrives. Note also that the accuracy of our guess is not critical, because we are going to verify it anyway. Figure 6-2 shows the different cases.
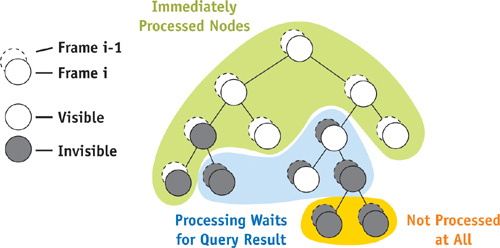
Figure 6-2 Processing Requirements for Various Nodes
6.5.2 Idea 2: Pull Up, Pull Up
To address problem 2, we need a way to reduce overhead caused by the occlusion queries for interior nodes.
Luckily, this is easy to solve. Using idea 1, we are already processing previously visible interior nodes without waiting for their query results anyway. It turns out that we don't even need to issue a query for these nodes, because at the end of the frame, this information can be easily deduced from the classification of its children, effectively "pulling up" visibility information in the tree. Therefore, we save a number of occlusion queries and a huge amount of fill rate.
On the other hand, occlusion queries for interior nodes that were occluded in the previous frame are essential. They are required to verify our choice not to process the node, and in case the choice was correct, we have saved rendering all the draw calls, geometry, and pixels that are below that node (that is, inside the bounding box of the node).
What this boils down to is that we issue occlusion queries only for previously visible leaf nodes and for the largest possible occluded nodes in the hierarchy (in other words, an occluded node is not tested if its parent is occluded as well). The number of queries issued is therefore linear in the number of visible objects. Figure 6-3 illustrates this approach.
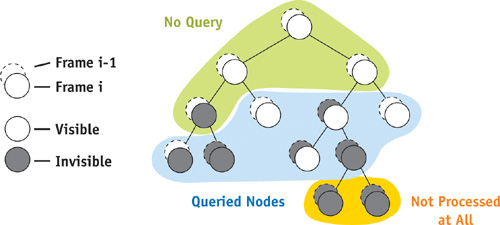
Figure 6-3 Occlusion Query Requirements for Various Nodes
6.5.3 Algorithm
We apply these two ideas in an algorithm we call "coherent hierarchical culling." In addition to the hierarchical data structure for the front-to-back traversal we already know, we need a "query queue" that remembers the queries we issued previously. We can then come back later to this queue to check whether the result for a query is already available.
The algorithm is easy to incorporate into any engine as it consists of a simple main traversal loop. A queue data structure is part of the C++ standard template library (STL), and a hierarchical data structure is part of most rendering libraries anyway; for example, for collision detection.
The algorithm visits the hierarchy in a front-to-back order and immediately recurses through any previously visible interior node (idea 1). For all other nodes, it issues an occlusion query and stores it in the query queue. If the node was a previously visible leaf node, it also renders it immediately, without waiting for the query result.
During the traversal of the hierarchy, we want to make sure that we incorporate the query results as soon as possible, so that we can issue further queries if we encounter a change in visibility.
Therefore, after each visited node, we check the query queue to see if a result has already arrived. Any available query result is processed immediately. Queries that verify our guess to be correct are simply discarded and do not generate additional work. Queries that contradict our guess are handled as follows: Nodes that were previously visible and became occluded are marked as such. Nodes that were previously occluded and became visible are traversed recursively (interior nodes) or rendered (leaf nodes). Both of these cases cause visibility information to be pulled up through the tree. See Figure 6-4, which also depicts a "pull-down" situation: a previously occluded node has become visible and its children need to be traversed.
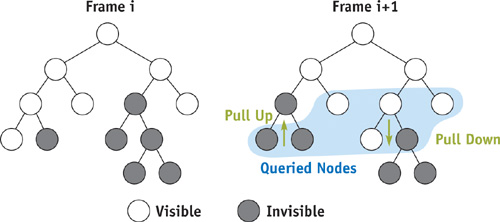
Figure 6-4 Visibility of Hierarchy Nodes in Two Consecutive Frames
6.5.4 Implementation Details
The algorithm is easy to follow using the pseudocode, which we show in Listing 6-1. Let's discuss some of the details in the code.
To maintain the visibility classification for all nodes over consecutive frames, we use a visible flag and a frameID, which increments every frame. Nodes visible in the previous frame are easily identified through lastVisited = frameID - 1 and visible = true; all other nodes are assumed invisible. This way, we don't have to reset the visibility classification for each frame.
Example 6-1. Algorithm Pseudocode
TraversalStack.Push(hierarchy.Root);
while (not TraversalStack.Empty() or not QueryQueue.Empty())
{
//--PART 1: process finished occlusion queries
while (not QueryQueue.Empty() and
(ResultAvailable(QueryQueue.Front()) or TraversalStack.Empty()))
{
node = QueryQueue.Dequeue();
// wait if result not available
visiblePixels = GetOcclusionQueryResult(node);
if (visiblePixels > VisibilityThreshold)
{
PullUpVisibility(node);
TraverseNode(node);
}
}
//--PART 2: hierarchical traversal
if (not TraversalStack.Empty())
{
node = TraversalStack.Pop();
if (InsideViewFrustum(node))
{
// identify previously visible nodes
wasVisible = node.visible and (node.lastVisited == frameID - 1);
// identify nodes that we cannot skip queries for
leafOrWasInvisible = not wasVisible or IsLeaf(node);
// reset node's visibility classification
node.visible = false;
// update node's visited flag
node.lastVisited = frameID;
// skip testing previously visible interior nodes
if (leafOrWasInvisible)
{
IssueOcclusionQuery(node);
QueryQueue.Enqueue(node);
}
// always traverse a node if it was visible
if (wasVisible)
TraverseNode(node);
}
}
}
TraverseNode(node)
{
if (IsLeaf(node))
Render(node);
else
TraversalStack.PushChildren(node);
}
PullUpVisibility(node)
{
while (not node.visible)
{
node.visible = true;
node = node.parent;
}
}To establish the new visibility classification for the current frame, we set all nodes we encounter during the traversal to invisible by default. Later, when a query identifies a node as visible, we "pull up" visibility; that is, we set all its ancestors to visible as well.
Interior nodes that were visible in the previous frame (that is, not leafOrWasInvisible) are nodes for which we skip occlusion queries altogether.
Traversing a node means rendering the node for leaf nodes or pushing its children onto the traversal stack so that they get rendered front to back.
We also assume that the Render() call renders an object only if it hasn't been rendered before (this can be checked using the frameID). This facilitates the code for previously visible objects: when we finally get the result of their visibility query, we can just process them again without introducing a special case or rendering them twice (since they have already been rendered immediately after their query was issued).
Another advantage is that we can reference objects in several nodes of the hierarchy, and they still get rendered only once if several of these nodes are visible.
Furthermore, we have to be careful with occlusion tests for nodes near the viewpoint. If the front faces of a bounding box get clipped by the near plane, no fragments are generated for the bounding box. Thus the node would be classified as occluded by the test, even though the node is most likely visible. To avoid this error for each bounding box that passes the view-frustum test, we should check whether any of its vertices is closer than the near plane. In such a case, the associated node should be set visible without issuing an occlusion query. Finally, note that for the occlusion queries, the actual node bounding boxes can be used instead of the (usually less tight) nodes of the spatial hierarchy.
6.5.5 Why Are There Fewer Stalls?
Let's take a step back and see what we have achieved with our algorithm and why.
The coherent hierarchical culling algorithm does away with most of the inefficient waiting found in the hierarchical stop-and-wait method. It does so by interleaving the occlusion queries with normal rendering, and avoiding the need to wait for a query to finish in most cases.
If the viewpoint does not move, then the only point where we actually might have to wait for a query result is at the end of the frame, when all the visible geometry is already rendered. Previously visible nodes are rendered right away without waiting for the results.
If the viewpoint does move, the only dependency occurs if a previously invisible node becomes visible. We obviously need to wait for this to be known in order to decide whether to traverse the children of the node. However, this does not bother us too much: most likely, we have some other work to do during the traversal. The query queue allows us to check regularly whether the result is available while we are doing useful work in between.
Note that in this situation, we might also not detect some occlusion situations and unnecessarily draw some objects. For example, if child A occludes child B of a previously occluded interior node, but the query for B is issued before A is rendered, then B is still classified as visible for the current frame. This happens when there is not enough work to do between issuing the queries for A and B. (See also Section 6.5.7, where we show how a priority queue can be used to increase the chance that there is work to do between the queries for A and B.)
6.5.6 Why Are There Fewer Queries?
We have already seen that a hierarchical occlusion-culling algorithm can save a lot of occlusion queries if large parts of the scene are occluded. However, this is paid for by large costs for testing interior nodes.
The coherent hierarchical culling algorithm goes a step further by obviating the need for testing most interior nodes. The number of queries that need to be issued is only proportional to the number of visible objects, not to the total number of objects in the scene. In essence, the algorithm always tests the largest possible nodes for occluded regions.
Neither does the number of queries depend on the depth of the hierarchy, as in the hierarchical stop-and-wait method. This is a huge win, because the rasterization of large interior nodes can cost more than occlusion culling buys.
6.5.7 How to Traverse the Hierarchy
We haven't talked a lot about traversing the hierarchy up to now. In principle, the traversal depends on which hierarchy we use, and is usually implemented with a traversal stack, where we push child nodes in front-to-back order when a node is traversed. This basically boils down to a depth-first traversal of the hierarchy.
However, we can gain something by not adhering to a strict depth-first approach. When we find nodes that have become visible, we can insert these nodes into the traversal, which should be compatible with the already established front-to-back order in the hierarchy.
The solution is not to use a traversal stack, but a priority queue based on the distance to the observer. A priority queue makes the front-to-back traversal very simple. Whenever the children of a node should be traversed, they are simply inserted into the priority queue. The main loop of the algorithm now just checks the priority queue, instead of the stack, for the next node to be processed.
This approach makes it simple to work with arbitrary hierarchies. The hierarchy only needs to provide a method to extract its children from a node, and to compute the bounding box for any node. This way, it is easy to use a sophisticated hierarchy such as a k-d tree (Cohen-Or et al. 2003), or just the bounding volume hierarchy of the scene graph for the traversal, and it is easy to handle dynamic scenes.
Note also that an occlusion-culling algorithm can be only as accurate as the objects on which it operates. We cannot expect to get accurate results for individual triangles if we only test nodes of a coarse hierarchy for occlusion. Therefore, the choice of a hierarchy plays a critical role in occlusion culling.
6.6 Optimizations
We briefly cover a few optimizations that are beneficial in some (but not all) scenes.
6.6.1 Querying with Actual Geometry
First of all, a very simple optimization that is always useful concerns previously visible leaf nodes (Sekulic 2004). Because these will be rendered regardless of the outcome of the query, it doesn't make sense to use an approximation (that is, a bounding box) for the occlusion query. Instead, when issuing the query as described in Section 6.3, we omit step 2 and replace step 3 by rendering the actual geometry of the object. This saves rasterization costs and draw calls as well as state changes for previously visible leaf nodes.
6.6.2 Z-Only Rendering Pass
For some scenes, using a z-only rendering pass can be advantageous for our algorithm. Although this entails twice the transformation cost and (up to) twice the draw calls for visible geometry, it provides a good separation between occlusion culling and rendering passes as far as rendering states are concerned. For the occlusion pass, the only state that needs to be changed between an occlusion query and the rendering of an actual object is depth writing. For the full-color pass, visibility information is already available, which means that the rendering engine can use any existing mechanism for optimizing state change overhead (such as ordering objects by rendering state).
6.6.3 Approximate Visibility
We might be willing to accept certain image errors in exchange for better performance. This can be achieved by setting the VisibilityThreshold in the algorithm to a value greater than zero. This means that nodes where no more than, say, 10 or 20 pixels are visible are still considered occluded. Don't set this too high, though; otherwise the algorithm culls potential occluders and obtains the reverse effect.
This optimization works best for scenes with complex visible geometry, where each additional culled object means a big savings.
6.6.4 Conservative Visibility Testing
Another optimization makes even more use of temporal coherence. When an object is visible, the current algorithm assumes it will also be visible for the next frame. We can even go a step further and assume that it will be visible for a number of frames. If we do that, we save the occlusion queries for these frames (we assume it's visible anyway). For example, if we assume an object remains visible for three frames, we can cut the number of required occlusion queries by almost a factor of three! Note, however, that temporal coherence does not always hold, and we almost certainly render more objects than necessary.
This optimization works best for deep hierarchies with simple leaf geometry, where the number of occlusion queries is significant and represents significant overhead that can be reduced using this optimization.
6.7 Conclusion
Occlusion culling is an essential part of any rendering system that strives to display complex scenes. Although hardware occlusion queries seem to be the long-sought-after solution to occlusion culling, they need to be used carefully, because they can introduce stalls into the rendering pipeline.
We have shown an algorithm that practically eliminates any waiting time for occlusion query results on both the CPU and the GPU. This is achieved by exploiting temporal coherence, assuming that objects that have been visible in the previous frame remain visible in the current frame. The algorithm also reduces the number of costly occlusion queries by using a hierarchy to cull large occluded regions using a single test. At the same time, occlusion tests for most other interior nodes are avoided.
This algorithm should make hardware occlusion queries useful for any application that features a good amount of occlusion, and where accurate images are important. For example, Figure 6-5 shows the application of the algorithm to the walkthrough of a city model, with the visibility classification of hierarchy nodes below. The orange nodes were found visible; all the other depicted nodes are invisible. Note the increasing size of the occluded nodes with increasing distance from the visible set. For the viewpoint shown, the algorithm presented in this chapter provided a speedup of about 4 compared to rendering with view-frustum culling alone, and a speedup of 2.6 compared to the hierarchical stop-and-wait method.

Figure 6-5 Visualizing the Benefits of Occlusion Queries for a City Walkthrough
6.8 References
Bittner, J., M. Wimmer, H. Piringer, and W. Purgathofer. 2004. "Coherent Hierarchical Culling: Hardware Occlusion Queries Made Useful." Computer Graphics Forum (Proceedings of Eurographics 2004) 23(3), pp. 615–624.
Cohen-Or, D., Y. Chrysanthou, C. Silva, and F. Durand. 2003. "A Survey of Visibility for Walkthrough Applications." IEEE Transactions on Visualization and Computer Graphics 9(3), pp. 412–431.
NVIDIA Corporation. 2004. NVIDIA GPU Programming Guide. http://developer.nvidia.com/object/gpu_programming_guide.html
Sekulic, D. 2004. "Efficient Occlusion Culling." In GPU Gems, edited by Randima Fernando, pp. 487–503. Addison-Wesley.
Wloka, M. 2003. "Batch, Batch, Batch: What Does It Really Mean?" Presentation at Game Developers Conference 2003. http://developer.nvidia.com/docs/IO/8230/BatchBatchBatch.pdf
Copyright
Many of the designations used by manufacturers and sellers to distinguish their products are claimed as trademarks. Where those designations appear in this book, and Addison-Wesley was aware of a trademark claim, the designations have been printed with initial capital letters or in all capitals.
The authors and publisher have taken care in the preparation of this book, but make no expressed or implied warranty of any kind and assume no responsibility for errors or omissions. No liability is assumed for incidental or consequential damages in connection with or arising out of the use of the information or programs contained herein.
NVIDIA makes no warranty or representation that the techniques described herein are free from any Intellectual Property claims. The reader assumes all risk of any such claims based on his or her use of these techniques.
The publisher offers excellent discounts on this book when ordered in quantity for bulk purchases or special sales, which may include electronic versions and/or custom covers and content particular to your business, training goals, marketing focus, and branding interests. For more information, please contact:
U.S. Corporate and Government Sales
(800) 382-3419
corpsales@pearsontechgroup.com
For sales outside of the U.S., please contact:
International Sales
international@pearsoned.com
Visit Addison-Wesley on the Web: www.awprofessional.com
Library of Congress Cataloging-in-Publication Data
GPU gems 2 : programming techniques for high-performance graphics and general-purpose
computation / edited by Matt Pharr ; Randima Fernando, series editor.
p. cm.
Includes bibliographical references and index.
ISBN 0-321-33559-7 (hardcover : alk. paper)
1. Computer graphics. 2. Real-time programming. I. Pharr, Matt. II. Fernando, Randima.
T385.G688 2005
006.66—dc22
2004030181
GeForce™ and NVIDIA Quadro® are trademarks or registered trademarks of NVIDIA Corporation.
Nalu, Timbury, and Clear Sailing images © 2004 NVIDIA Corporation.
mental images and mental ray are trademarks or registered trademarks of mental images, GmbH.
Copyright © 2005 by NVIDIA Corporation.
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form, or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior consent of the publisher. Printed in the United States of America. Published simultaneously in Canada.
For information on obtaining permission for use of material from this work, please submit a written request to:
Pearson Education, Inc.
Rights and Contracts Department
One Lake Street
Upper Saddle River, NJ 07458
Text printed in the United States on recycled paper at Quebecor World Taunton in Taunton, Massachusetts.
Second printing, April 2005
Dedication
To everyone striving to make today's best computer graphics look primitive tomorrow
- Copyright
- Inside Back Cover
- Inside Front Cover
- Part I: Geometric Complexity
-
- Chapter 1. Toward Photorealism in Virtual Botany
- Chapter 2. Terrain Rendering Using GPU-Based Geometry Clipmaps
- Chapter 3. Inside Geometry Instancing
- Chapter 4. Segment Buffering
- Chapter 5. Optimizing Resource Management with Multistreaming
- Chapter 6. Hardware Occlusion Queries Made Useful
- Chapter 7. Adaptive Tessellation of Subdivision Surfaces with Displacement Mapping
- Chapter 8. Per-Pixel Displacement Mapping with Distance Functions
- Part II: Shading, Lighting, and Shadows
-
- Chapter 9. Deferred Shading in S.T.A.L.K.E.R.
- Chapter 10. Real-Time Computation of Dynamic Irradiance Environment Maps
- Chapter 11. Approximate Bidirectional Texture Functions
- Chapter 12. Tile-Based Texture Mapping
- Chapter 13. Implementing the mental images Phenomena Renderer on the GPU
- Chapter 14. Dynamic Ambient Occlusion and Indirect Lighting
- Chapter 15. Blueprint Rendering and "Sketchy Drawings"
- Chapter 16. Accurate Atmospheric Scattering
- Chapter 17. Efficient Soft-Edged Shadows Using Pixel Shader Branching
- Chapter 18. Using Vertex Texture Displacement for Realistic Water Rendering
- Chapter 19. Generic Refraction Simulation
- Part III: High-Quality Rendering
-
- Chapter 20. Fast Third-Order Texture Filtering
- Chapter 21. High-Quality Antialiased Rasterization
- Chapter 22. Fast Prefiltered Lines
- Chapter 23. Hair Animation and Rendering in the Nalu Demo
- Chapter 24. Using Lookup Tables to Accelerate Color Transformations
- Chapter 25. GPU Image Processing in Apple's Motion
- Chapter 26. Implementing Improved Perlin Noise
- Chapter 27. Advanced High-Quality Filtering
- Chapter 28. Mipmap-Level Measurement
- Part IV: General-Purpose Computation on GPUS: A Primer
-
- Chapter 29. Streaming Architectures and Technology Trends
- Chapter 30. The GeForce 6 Series GPU Architecture
- Chapter 31. Mapping Computational Concepts to GPUs
- Chapter 32. Taking the Plunge into GPU Computing
- Chapter 33. Implementing Efficient Parallel Data Structures on GPUs
- Chapter 34. GPU Flow-Control Idioms
- Chapter 35. GPU Program Optimization
- Chapter 36. Stream Reduction Operations for GPGPU Applications
- Part V: Image-Oriented Computing
-
- Chapter 37. Octree Textures on the GPU
- Chapter 38. High-Quality Global Illumination Rendering Using Rasterization
- Chapter 39. Global Illumination Using Progressive Refinement Radiosity
- Chapter 40. Computer Vision on the GPU
- Chapter 41. Deferred Filtering: Rendering from Difficult Data Formats
- Chapter 42. Conservative Rasterization
- Part VI: Simulation and Numerical Algorithms
-
- Chapter 43. GPU Computing for Protein Structure Prediction
- Chapter 44. A GPU Framework for Solving Systems of Linear Equations
- Chapter 45. Options Pricing on the GPU
- Chapter 46. Improved GPU Sorting
- Chapter 47. Flow Simulation with Complex Boundaries
- Chapter 48. Medical Image Reconstruction with the FFT