NVIDIA cuOpt 是一款 GPU 加速的优化引擎,旨在为大规模复杂决策问题提供高效、高质量的解决方案。 混合整数规划(MIP) 是一种求解问题的技术,可通过一组线性约束进行建模,其中部分变量仅能取整数值。可建模为 MIP 的问题类型十分广泛,涵盖 生产规划、 供应链、运输、调度以及 财务.
NVIDIA cuOpt 是一款 GPU 加速的求解器,专为大规模约束密集型问题提供低延迟、高质量的优化方案。cuOpt 的核心采用混合整数编程(MIP),通过线性约束将决策建模为包含连续变量和整数变量的优化问题。这使其在供应链网络优化、路径规划与调度、劳动力与任务分配、生产计划以及量化金融等领域具有广泛的应用价值。
适用于 MIP 求解器的加速原始启发式算法无需对整个求解空间进行彻底搜索,即可提供高质量且可行的解决方案。其必要性主要体现在两个方面。一方面,许多现实世界中的 MIP 问题规模庞大或具有较强的时间敏感性,传统求解器难以在有限时间内得出结果;另一方面,这类算法有助于缩减分支定界算法的搜索空间。加速启发式算法通过采用并行计算和更高效的搜索策略,显著缩短了求解时间,使企业能够快速响应突发情况并实现低延迟决策。
本文介绍了 NVIDIA cuOpt 如何利用 GPU 加速,结合原始启发式算法为 MIP 问题提供高质量解决方案,从而在 MIPLIB 基准集的四个开放实例——liu.mps、neos-3355120-tarago.mps、polygonpack4-7.mps 和 bts4-cta.mps 中,成功发现新的可行解。实验结果表明,相较于领先的开源 CPU 求解器,其在解的质量和可行解数量方面均有显著提升通过原始启发式算法。
为何快速且高质量的解决方案对大规模 MIP 至关重要
MIP 是一类 NP-hard 问题的子集,这意味着在最坏情况下,任何已知算法都无法高效求解所有此类问题。然而,尽管 MIP 具有 NP – Hard 特性,商业 MIP 求解器通常仍能为许多大规模实例提供最优解。
但是,某些问题仍然难以解决,或者需要耗费较长的计算时间。鉴于混合整数规划(MIP)能够对现实世界的问题进行建模,并且其求解结果通常直接关联到运营成本,因此开发能够高效处理日益庞大和复杂实例的算法,一直是该领域的重要目标(可追溯至20世纪中叶)。自那时以来,我们在理论与计算方面取得了诸多重要突破,包括分支定界算法、割平面方法、原始启发式算法(如可行性泵),以及近年来的并行处理技术。
现实世界的问题通常是动态的,输入会随着时间推移而发生变化。这要求求解器采用迭代和增量方法,使得每一步的求解速度都至关重要。具有时间压力的混合整数规划问题包括灵活的作业车间调度及其变体、批量大小决策,以及航空公司或铁路乘务人员调度等。因此,在 cuOpt 中,我们投入了大量精力开发原始启发式算法,以在短时间内快速找到高质量的解决方案,其求解速度通常优于其他开源求解器。
如何获得适用于 MIP 的高质量可行解
迄今为止,极为成功的原始启发式算法之一是可行性泵(FP),每年都会涌现基于这一思想的新论文。其核心理念相对简单:通过域传播,在可行区域的投影与保持分数特性的舍入变量之间进行迭代。
我们首先优化现有算法,以进一步提升 GPU 性能,并解决 FP 算法的两个主要瓶颈:
- 投影被建模为线性规划问题。
- 投影后的域进行传播。
我们观察到,FP 算法中投影的精度并不关键,因为即使精度较低,也能获得相近的结果。这启发我们考虑采用一阶方法来替代单纯形算法,幸运的是,PDLP(Primal-Dual 混合梯度)已在 cuOpt 框架中实现。
我们利用上一次投影的原始解和二元解来初始化 PDLP 算法。在可行域预处理(FP)和根节点中应用 PDLP,使我们能够加快迭代速度,并更高效地求解更大规模的问题。为应对第二个瓶颈,我们实现了域传播算法的 GPU 版本,并引入了批量舍入和动态变量排序等显著优化。在消除这些瓶颈后,我们的工作重点转向了去除可行域预处理中的循环现象。
循环是重复步骤的问题,通常通过引入随机性以探索搜索空间的不同区域来解决。相比之下,我们选择采用 Local-MIP 算法来打破循环,同时优化目标。为高效实现这一方法,我们在 GPU 上实现了 Local-MIP,其性能优于标准 CPU 版本。
我们还在每次迭代中加入了目标截止值,并发现了一种可行的新解决方案,相关成果已发表于论文中。
这些改进为寻找可行的解决方案提供了先进的原始启发式算法。下表展示了我们的方法与近期 FP 变体及 Local-MIP 在可行解数量(3 次运行的平均值)和目标差距(基准解与启发式算法所找到解之间的归一化差异)方面的对比:
| 方法 | 平均。* 可行 | 原始差距 |
| 修复和传播投资组合默认 | 193.8 | 0.66 |
| Local-MIP | 188.67 | 0.46 |
| GPU Local-MIP | 205 | 0.41 |
| GPU 扩展浮点,采用最近舍入 | 220 | 0.23 |
| GPU 扩展浮点,结合修复与传播 | 220.67 | 0.22 |
除了这些增强功能之外,我们还引入了三种新的进化算法,以进一步优化模型。当检测到搜索停滞时,这些算法可将原始间隙再降低 3%。通过将简单的分支定界方法(不包含切割平面)与潜水线程以及基于 subMIP 的进化算法相结合,实现了更显著的改进。接下来,我们将该方法与广泛使用的开源求解器进行比较:
MIP 求解器基准测试
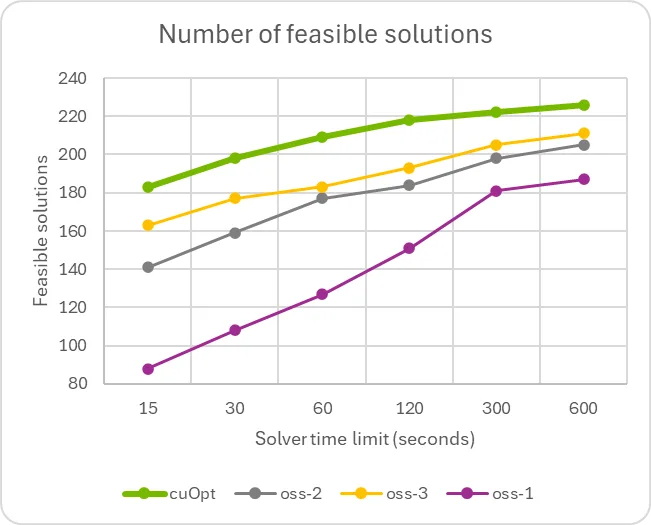
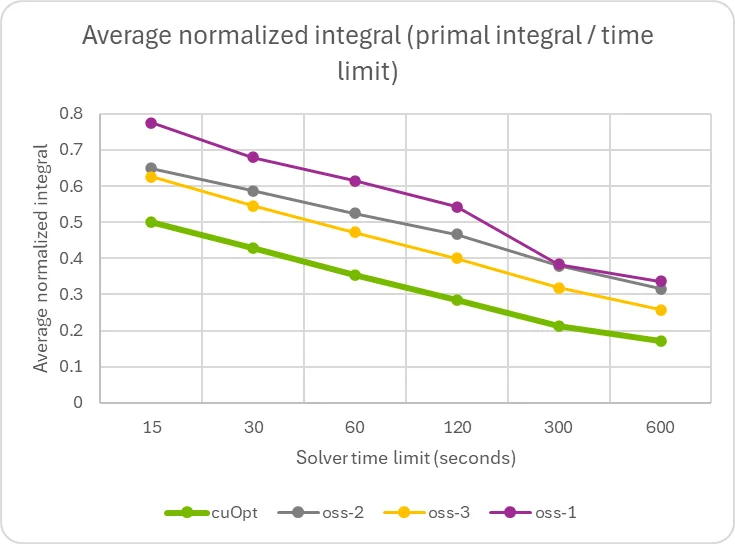
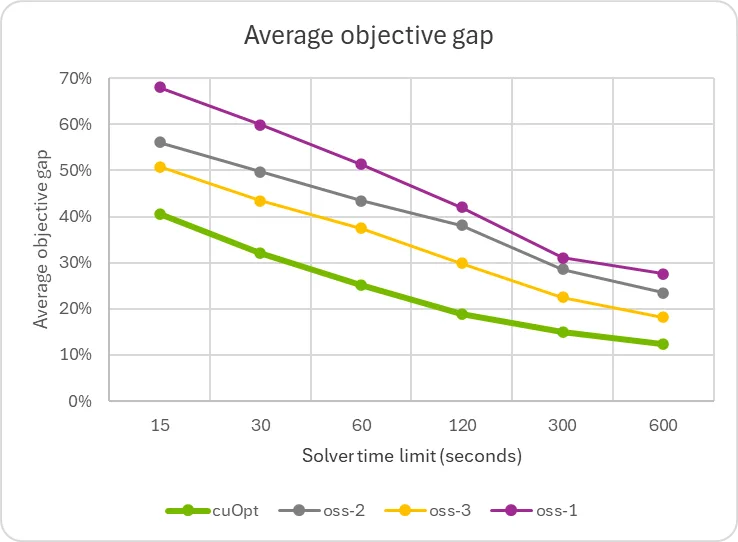
本图显示,与采用复杂的切割平面算法和特定问题方法的求解器相比,求解器的求解速度显著提升。这表明仍存在进一步改进的潜力,并且有可能通过此前详细介绍的 GPU 加速的原始启发式算法,来增强任何现有的求解器。
GPU 如何让 MIP 求解变得切实可行
快速、可行的 MIP 求解在决策智能流程中发挥着关键作用。当与 Palantir Ontology 和 NVIDIA Nemotron 推理智能体等系统集成时,能够并行生成和评估多种操作场景。cuOpt 中的开源 GPU 加速 MIP 求解器可在几秒钟内计算出可行解,使下游智能体得以模拟不同方案,并在环境变化时快速重新优化计划。该能力可将静态优化转变为持续反馈的过程,从而支持大规模的自适应决策。
MIP 启发式求解器能够提供快速可行的解决方案,无需全面探索问题空间。
这使得组织可以迅速测试多种替代方案,并有效应对现实中的突发情况,例如港口延迟、设备故障或需求激增。NVIDIA cuOpt 借助 GPU 加速,使这些启发式算法在大规模场景下变得切实可行,从而加快求解速度、缩小与最优解之间的差距,并支持持续的自适应决策过程。欢迎访问 NVIDIA cuOpt GitHub 进行实验,并尝试针对优化问题的 MIP 应用示例。





