随着量子处理器 (QPU) 性能的提升,模拟大规模量子计算机变得愈发困难。验证结果是确保在设备规模超出经典可模拟范围后,我们仍然能够信任其输出的关键。
同样,在为旨在协助运行量子处理器的各类 AI 模型生成大规模数据集时,我们发现需要提供由 GPU 加速、涵盖不同规模与抽象层次的实用训练数据。示例包括用于量子纠错的 AI 解码器、AI 编译器、用于校准与控制的 AI 智能体,以及用于生成新型器件设计的模型。
cuQuantum SDK 是一组高性能库和工具,可将电路和设备级别的量子计算模拟加速几个数量级。新版 cuQuantum SDK, v25.11 引入了可加速两种新工作负载的组件:Pauli 传播和稳定器仿真。每一种都对模拟大规模量子计算机至关重要。
本文将深入探讨如何启动 Pauli 传播仿真,并加速从稳定器仿真中的采样过程,从而利用 GPU 加速的超级计算机高效解决相关问题。
cuQuantum cuPauliProp
Pauli 传播是一种较新的方法,可用于高效模拟大规模量子电路中的可观测量,且能够包含真实量子处理器的噪声模型。该方法将量子态和可观测量表示为 Pauli 张量积的加权和,从而在电路模拟过程中动态舍弃对期望值贡献较小的项。这使得估算那些难以通过精确模拟获得的实验结果成为可能。
许多相关的量子计算应用都以期望值的计算为核心,例如变分量子本征求解器(VQE)和物理动力学的量子模拟。尽管存在多种精确和近似的经典模拟技术可用于计算大型电路中的此类可观测值,但在不同设置下,这些方法的计算成本可能变得极高。例如,矩阵乘积态技术作为一种广受欢迎的近似张量网络态方法,通常难以有效编码用于模拟二维或三维物理系统动力学的大型电路。对于理想电路和含噪声电路,Pauli 传播为现有的近似电路模拟工具箱提供了有力补充。除了在模拟接近Clifford电路或高度随机电路方面具备可证明的高效性之外,Pauli 传播在模拟某些量子自旋系统演化所对应的电路时也展现出卓越性能。其中包括一些被称为“实用电路”的实例,其命名参考了IBM在127量子比特设备上开展的可用性实验,相关成果详见Evidence for the Utility of Quantum Computing Before Fault Tolerance。明确哪些电路能够通过Pauli 传播实现高效模拟,是一项持续进行的研究课题,其重要性不亚于对方法本身算法细节的优化与完善。随着这一全新cuQuantum库的发布,cuQuantum 25.11 提供了在NVIDIA GPU上加速 Pauli 传播及其衍生方法的基本构件,使开发者和研究人员能够推动该领域技术的前沿发展。后续章节将介绍其核心功能。
库初始化
初始化操作所需的库句柄与工作空间描述符:
import cupy as cp
from cuquantum.bindings import cupauliprop
from cuquantum import cudaDataType
# Create library handle and workspace descriptor
handle = cupauliprop.create()
workspace = cupauliprop.create_workspace_descriptor(handle)
# Assign GPU memory to workspace
ws_size = 1024 * 1024 * 64 # Example: 64 MiB
d_ws = cp.cuda.alloc(ws_size)
cupauliprop.workspace_set_memory(
handle, workspace, cupauliprop.Memspace.DEVICE,
cupauliprop.WorkspaceKind.WORKSPACE_SCRATCH, d_ws.ptr, ws_size
)
定义可观察对象
要开始模拟,请为 Pauli 扩展分配设备内存(将 Pauli 算子的乘积之和表示为一组无符号整数及其对应的系数),并使用可观察量初始化输入扩展(例如,
)。
# Helper to encode Pauli string into packed integers (2 bits per qubit: X and Z masks)
def encode_pauli(num_qubits, paulis, qubits):
num_ints = cupauliprop.get_num_packed_integers(num_qubits)
# Packed integer format: [X_ints..., Z_ints...]
packed = np.zeros(num_ints * 2, dtype=np.uint64)
x_mask, z_mask = packed[:num_ints], packed[num_ints:]
for p, q in zip(paulis, qubits):
idx, bit = divmod(q, 64)
if p in (cupauliprop.PauliKind.PAULI_X, cupauliprop.PauliKind.PAULI_Y):
x_mask[idx] |= (1 << bit)
if p in (cupauliprop.PauliKind.PAULI_Z, cupauliprop.PauliKind.PAULI_Y):
z_mask[idx] |= (1 << bit)
return packed
# 1. Allocate Device Buffers
# Define capacity (max number of Pauli strings) and allocate buffers
max_terms = 10000
num_packed_ints = cupauliprop.get_num_packed_integers(num_qubits)
d_pauli = cp.zeros((max_terms, 2 * num_packed_ints), dtype=cp.uint64, order="C")
d_coef = cp.zeros(max_terms, dtype=cp.float64, order="C")
# 2. Populate Initial Observable (Z_62)
encoded_pauli = encode_pauli(num_qubits, [cupauliprop.PauliKind.PAULI_Z], [62])
# Assign the first term
d_pauli[0] = cp.array(encoded_pauli)
d_coef[0] = 1.0
# 3. Create Pauli Expansions
# Input expansion: pre-populated with our observable
expansion_in = cupauliprop.create_pauli_expansion(
handle, num_qubits,
d_pauli.data.ptr, d_pauli.nbytes,
d_coef.data.ptr, d_coef.nbytes,
cudaDataType.CUDA_R_64F,
1, 1, 1 # num_terms=1, is_sorted=True, is_unique=True
)
# Output expansion: empty initially (num_terms=0), needs its own buffers
d_pauli_out = cp.zeros_like(d_pauli)
d_coef_out = cp.zeros_like(d_coef)
expansion_out = cupauliprop.create_pauli_expansion(
handle, num_qubits,
d_pauli_out.data.ptr, d_pauli_out.nbytes,
d_coef_out.data.ptr, d_coef_out.nbytes,
cudaDataType.CUDA_R_64F,
0, 0, 0
)
Operator 创建
定义量子门或算子,例如 Pauli 旋转
。
# Create a Z-rotation gate on qubit 0
paulis = [cupauliprop.PauliKind.PAULI_Z]
qubits = [0]
gate = cupauliprop.create_pauli_rotation_gate_operator(
handle, theta, 1, qubits, paulis
)
Operator 应用
将操作员(门或噪声通道)应用到扩展程序中,以改进系统。请注意,大多数应用程序在所谓的海森堡绘景(Heisenberg Picture)中运行,这意味着电路中的门会以相反顺序作用于可观测量。在应用算符时,还需将 adjoint 参数传递为 True。
# Get a view of the current terms in the input expansion
num_terms = cupauliprop.pauli_expansion_get_num_terms(handle, expansion_out)
view = cupauliprop.pauli_expansion_get_contiguous_range(
handle, expansion_in, 0, num_terms)
# Apply gate: in_expansion -> gate -> out_expansion
cupauliprop.pauli_expansion_view_compute_operator_application(
handle, view, expansion_out, gate,
True, # adjoint?
False, False, # make_sorted?, keep_duplicates?
0, None, # Truncation strategies (optional)
workspace
)
期望值
计算期望值(使用零状态
进行追踪)。
import numpy as np
result = np.zeros(1, dtype=np.float64)
# Compute trace
cupauliprop.pauli_expansion_view_compute_trace_with_zero_state(
handle, view, result.ctypes.data, workspace
)
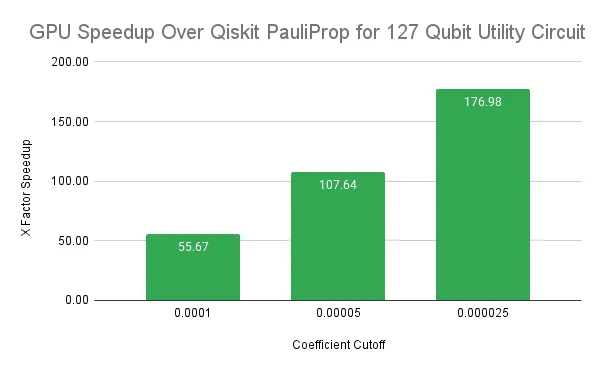
结合使用这些方法表明,与基于 CPU 的代码相比,NVIDIA DGX B200 GPU 的速度显著提升。对于较小的系数截止值,在新一代双路数据中心 CPU 上,单线程 Qiskit Pauli-Prop 的加速达到多个数量级。

cuQuantum cuStabilizer
Gottesman-Knill 定理(Gottesman-Knill theorem)提出了稳定器模拟,指出 Clifford 群(量子位 Pauli 群的归一化子群)中的量子门可以在多项式时间内通过经典计算机高效模拟。该 Clifford 群由 CNOT 门、Hadamard 门以及相位门(S)构成。因此,稳定器模拟在资源估算以及大规模量子纠错码的验证中具有重要作用。
从画面模拟器到帧模拟器,构建稳定器模拟器有多种不同的方法。cuStabilizer 目前用于提升帧模拟器中采样率的吞吐量。
帧模拟仅关注量子噪声对量子态的影响。由于量子设备存在不完美性,可通过在电路中插入随机的“噪声”门来模拟执行过程中的缺陷。若已知无噪声情况下的结果,则只需追踪噪声门如何改变电路输出,即可获得含噪声的结果。
事实证明,与全电路模拟相比,这种效应的计算要容易得多。随着电路规模的增大,噪声门插入方式的可能组合数量会迅速增加,这意味着为了可靠地建模纠错算法,需要大量的样本。
对于有兴趣开发量子纠错码、测试新解码器或为 AI 解码器生成数据的用户而言,帧模拟是理想的选择。该 API 可用于改进采样,并加速在 NVIDIA GPU 上运行的任何帧模拟任务。cuQuantum SDK 的 cuStabilizer 库提供 C API 和 Python API。其中,C API 能提供更优的性能,而 Python API 则更适合初学者,因其具备更高的灵活性,并支持用户自主管理内存分配。
创建电路并应用帧模拟
cuStabilizer 的仿真主要包含两类: Circuit 和 FrameSimulator 。电路能够接收包含电路指令的字符串,类似于 Stim CPU 模拟器所采用的格式。要创建 FrameSimulator ,需指定电路的相关信息,以便分配充足的资源。
import cuquantum.stabilizer as cust
# Circuit information
num_qubits = 5
num_shots = 10_000
num_measurements = 2
# Create a circuit on GPU
circ = cust.Circuit("""
H 0 1
X_ERROR(0.1) 1 2
DEPOLARIZE2(0.5) 2 3
CX 0 1 2 3
M 0 3
"""
sim = cust.FrameSimulator(
num_qubits,
num_shots,
num_measurements
)
sim.apply(circ)
您可以在不同电路之间重复使用模拟器,只要模拟器具备足够的可用量子位。以下代码会将电路应用到由第一个电路 circ 所修改的态上。
circ2 = cust.Circuit("""
Z_ERROR(0.01) 1 4
""")
sim.apply(circ2)
读取模拟结果
模拟器的状态由三个位表构成:
- x_bits
- z_bits
- measurement_bits
前两个表用于存储 Pauli 帧(类似于 cuPauliProp Pauli 扩展,但采用不同的布局且不包含权重)。第三个表用于存储每个镜头中无噪声测量值与有噪声测量值之间的差异。
存储位的高效方法是将其编码为整数值。这被称为“位填充”格式,其中内存中的每个字节都存储 8 个重要位。尽管这种格式效率较高,但处理单个位元需要在程序中执行额外的步骤。位填充格式不容易与“数组”的常见概念集成,因为数组通常被视为包含多个字节的值,例如 int32。
为了在 numpy 中实现简洁的表示,cuStabilizer 支持 bit_packed 参数,该参数可用于在不同格式之间切换。若设置为 bit_packed=False,每个位元将被编码为一个 uint8 值,因此内存占用量会增加 8 倍。如 cuQuantum 文档 所述,指定输入位表时,格式对性能也有重要影响。
# Get measurement flips
m_table = sim.get_measurement_bits(bit_packed=False)
print(m_table.dtype)
# uint8
print(m_table.shape)
# (2, 10000)
print(m_table)
# [[0 0 0 ... 0 0 0]
# [1 0 0 ... 0 1 1]]
x_table, z_table = sim.get_pauli_xz_bits(bit_packed=True)
print(x_table.dtype)
# uint8
print(x_table.shape)
# (5, 1252)
为方便访问底层 Pauli 帧,cuStabilizer 提供了一个 PauliTable 类,哪可以通过镜头索引进行索引:
# Get pauli table
pauli_table = sim.get_pauli_table()
num_frames_print = 5
for i in range(num_frames_print):
print(pauli_table[i])
# ...XZ
# ZXX..
# ...Z.
# .....
# ...Z.
利用采样 API 时,我们发现,与 Google Stim(搭载于新一代数据中心 CPU 的先进代码)相比,能够显著提升吞吐量。
表面代码仿真
cuStabilizer 可以接收 Stim 电路作为输入,您可利用它来模拟表面码电路:
import stim
p = 0.001
circ_stim = stim.Circuit.generated(
"surface_code:rotated_memory_z",
distance=5,
rounds=5,
after_clifford_depolarization=p,
after_reset_flip_probability=p,
before_measure_flip_probability=p,
before_round_data_depolarization=p,
)
circ = cust.Circuit(circ_stim)
sim = cust.FrameSimulator(
circ_stim.num_qubits,
num_shots,
circ_stim.num_measurements,
num_detectors=circ_stim.num_detectors,
)
sim.apply(circ)
pauli_table = sim.get_pauli_table()
for i in range(num_frames_print):
print(pauli_table[i])
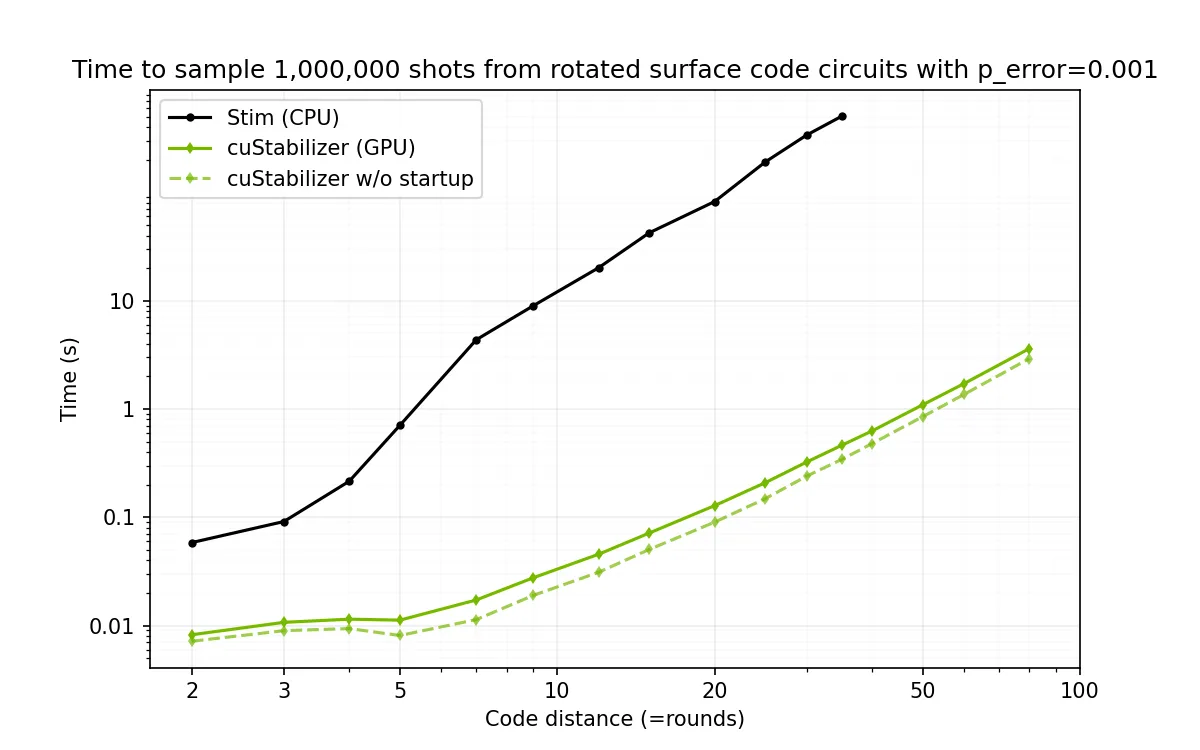
请注意,对于大量样本和数量众多的量子位,模拟效率较高。此外,当生成的位表保留在 GPU 上时,例如使用 cupy 包,能够实现更优的性能。
图 2 展示了 cuStabilizer 在 NVIDIA B200 GPU 和英特尔至强 Platinum 8570 CPU 上的理想使用情况与预期性能。结果显示,代码距离为 31 时,性能在约一百万个镜头的规模下达到较优水平。对于更大的代码距离,用户可获得高达 1060 倍的加速效果。

开始使用新的 cuQuantum 库
cuQuantum 中的新功能持续突破基于 GPU 的量子计算机仿真的极限,推动实现两种全新的主要工作负载类别。这些工作负载对中大规模量子设备的量子纠错、验证与确认,以及算法工程具有重要意义。
开始使用 pip install cupauliprop-cu13 运行 cuQuantum cuPauliProp。详情请参阅 cuPauliProp 文档。
开始使用 pip install custabilizer-cu13 运行 cuQuantum cuStabilizer。详情请参阅 cuStabilizer 文档。





