
GPU Gems 3
GPU Gems 3 is now available for free online!
The CD content, including demos and content, is available on the web and for download.
You can also subscribe to our Developer News Feed to get notifications of new material on the site.
Chapter 24. The Importance of Being Linear
Larry Gritz
NVIDIA Corporation
Eugene d'Eon
NVIDIA Corporation
24.1 Introduction
The performance and programmability of modern GPUs allow highly realistic lighting and shading to be achieved in real time. However, a subtle nonlinear property of almost every device that captures or displays digital images necessitates careful processing of textures and frame buffers to ensure that all this lighting and shading is computed and displayed correctly. Proper gamma correction is probably the easiest, most inexpensive, and most widely applicable technique for improving image quality in real-time applications.
24.2 Light, Displays, and Color Spaces
24.2.1 Problems with Digital Image Capture, Creation, and Display
If you are interested in high-quality rendering, you might wonder if the images displayed on your CRT, LCD, film, or paper will result in light patterns that are similar enough to the "real world" situation so that your eye will perceive them as realistic. You may be surprised to learn that there are several steps in the digital image creation pipeline where things can go awry. In particular:
- Does the capture of the light (by a camera, scanner, and so on) result in a digital image whose numerical values accurately represent the relative light levels that were present? If twice as many photons hit the sensor, will its numerical value be twice as high?
- Does a producer of synthetic images, such as a renderer, create digital images whose pixel values are proportional to what light would really do in the situation they are simulating?
- Does the display accurately turn the digital image back into light? If a pixel's numerical value is doubled, will the CRT, LCD, or other similar device display an image that appears twice as bright?
The answer to these questions is, surprisingly, probably not. In particular, both the capture (scanning, painting, and digital photography) and the display (CRT, LCD, or other) are likely not linear processes, and this can lead to incorrect and unrealistic images if care is not taken at these two steps of the pipeline.
The nonlinearity is subtle enough that it is often unintentionally or intentionally ignored, particularly in real-time graphics. However, its effects on rendering, particularly in scenes with plenty of dynamic range like Figure 24-1, are quite noticeable, and the simple steps needed to correct it are well worth the effort.
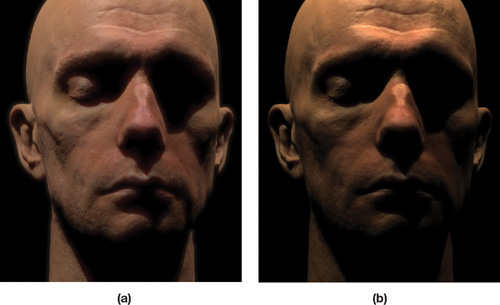
Figure 24-1 The Benefit of Proper Gamma Correction
24.2.2 Digression: What Is Linear?
In the mathematical sense, a linear transformation is one in which the relationship between inputs and outputs is such that:
- The output of the sum of inputs is equal to the sum of the outputs of the individual inputs. That is, f (x + y) = f (x) + f (y).
- The output scales by the same factor as a scale of the input (for a scalar k): f(k x x) = k x f (x).
Light transport is linear. The illumination contributions from two light sources in a scene will sum. They will not multiply, subtract, or interfere with each other in unobvious ways. [1]
24.2.3 Monitors Are Nonlinear, Renderers Are Linear
CRTs do not behave linearly in their conversion of voltages into light intensities. And LCDs, although they do not inherently have this property, are usually constructed to mimic the response of CRTs.
A monitor's response is closer to an exponential curve, as shown in Figure 24-2, and the exponent is called gamma. A typical gamma of 2.2 means that a pixel at 50 percent intensity emits less than a quarter of the light as a pixel at 100 percent intensity—not half, as you would expect! Gamma is different for every individual display device, [2] but typically it is in the range of 2.0 to 2.4. Adjusting for the effects of this nonlinear characteristic is called gamma correction.
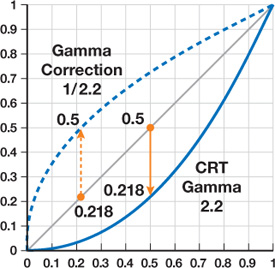
Figure 24-2 Typical Response Curve of a Monitor
Note that regardless of the exponent applied, the values of black (zero) and white (one) will always be the same. It's the intermediate, midtone values that will be corrected or distorted.
Renderers, shaders, and compositors like to operate with linear data. They sum the contributions of multiple light sources and multiply light values by reflectances (such as a constant value or a lookup from a texture that represents diffuse reflectivity).
But there are hidden assumptions—such as, that a texture map that indicates how reflectivity varies over the surface also has a linear scale. Or that, upon display, the light intensities seen by the viewer will be indeed proportional to the values the renderer stored in the frame buffer.
The point is, if you have nonlinear inputs, then a renderer, shader, or compositor will "do the math wrong." This is an impediment to achieving realistic results.
Consider a digital painting. If you weren't viewing with "proper gamma correction" while you were creating the painting, the painting will contain "hidden" nonlinearities. The painting may look okay on your monitor, but it may appear different on other monitors and may not appear as you expected if it's used in a 3D rendering. The renderer will not actually use the values correctly if it assumes the image is linear. Also, if you take the implicitly linear output of a renderer and display it without gamma correction, the result will look too dark—but not uniformly too dark, so it's not enough to just make it brighter.
If you err on both ends of the imaging pipeline—you paint or capture images in gamma (nonlinear) space, render linear, and then fail to correct when displaying the rendered images—the results might look okay at first glance. Why? Because the nonlinear painting/capture and the nonlinear display may cancel each other out to some degree. But there will be subtle artifacts riddled through the rendering and display process, including colors that change if a nonlinear input is brightened or darkened by lighting, and alpha-channel values that are wrong (compositing artifacts), and so your mipmaps were made wrong (texture artifacts). Plus, any attempts at realistic lighting—such as high dynamic range (HDR) and imaged-based lighting—are not really doing what you expect.
Also, your results will tend to look different for everybody who displays them because the paintings and the output have both, in some sense, a built-in reference to a particular monitor—and not necessarily the same monitors will be used for creating the paintings and 3D lighting!
24.3 The Symptoms
If you ignore the problem—paint or light in monitor space and display in monitor space—you may encounter the following symptoms.
24.3.1 Nonlinear Input Textures
The average user doesn't have a calibrated monitor and has never heard of gamma correction; therefore, many visual materials are precorrected for them. For example, by convention, all JPEG files are precorrected for a gamma of 2.2. That's not exact for any monitor, but it's in the ballpark, so the image will probably look acceptable on most monitors. This means that JPEG images (including scans and photos taken with a digital camera) are not linear, so they should not be used as texture maps by shaders that assume linear input.
This precorrected format is convenient for directly displaying images on the average LCD or CRT display. And for storage of 8-bit images, it affords more "color resolution" in the darks, where the eye is more sensitive to small gradations of intensity. However, this format requires that these images be processed before they are used in any kind of rendering or compositing operation.
24.3.2 Mipmaps
When creating a mipmap, the obvious way to downsize at each level is for each lower-mip texel to be one-fourth the sum of the four texels "above" it at the higher resolution. Suppose at the high-resolution level you have an edge: two pixels at 1.0 and two at 0.0. The low-resolution pixel ought to be 0.5, right? Half as bright, because it's half fully bright and half fully dark? And that's surely how you're computing the mipmap. Aha, but that's linear math. If you are in a nonlinear color space with a gamma, say of 2.0, then that coarse-level texel with a value of 0.5 will be displayed at only 25 percent of the brightness. So you will see not-so-subtle errors in low-resolution mipmap levels, where the intensities simply aren't the correctly filtered results of the high-resolution levels. The brightness of rendered objects will change along contour edges and with distance from the 3D camera.
Furthermore, there is a subtle problem with texture-filtering nonlinear textures on the GPU (or even CPU renderers), even if you've tried to correct for nonlinearities when creating the mipmaps. The GPU uses the texture lookup filter extents to choose a texture level of detail (LOD), or "mipmap level," and will blend between two adjacent mipmap levels if necessary. We hope by now you've gotten the gist of our argument and understand that if the render-time blend itself is also done assuming linear math—and if the two texture inputs are nonlinear—the results won't quite give the right color intensities. This situation will lead to textures subtly pulsating in intensity during transitions between mipmap levels.
24.3.3 Illumination
Consider the illumination of a simple Lambertian sphere, as shown in Figure 24-3. [3] If the reflected light is proportional to N · L, then a spot A on the sphere where N and L form a 60-degree angle should reflect half the light toward the camera. Thus, it appears half as bright as a spot B on the sphere, where N points straight to the light source. If these image values were converted to light linearly, when you view the image it should look like a real object with those reflective properties. But if you display the image on a monitor with a gamma of 2.0, A will actually only be 0.5 gamma , or one-fourth as bright as B.

Figure 24-3 A Linear Image Gamma-Corrected () and Uncorrected ()
In other words, computer-generated (CG) materials and lights will simply not match the appearance of real materials and lights if you render assuming linear properties of light but display on a nonlinear monitor. Overall, the scene will appear dimmer than an accurate simulation. However, merely brightening it by a constant factor is not good enough: The brights will be more correct than the midrange intensities. Shadow terminators and intensity transitions will be sharper—for example, the transition from light to dark will be faster—than in the real world. Corners will look too dark. And the more "advanced" lighting techniques that you use (such as HDR, global illumination of any kind, and subsurface scattering), the more critical it will become to stick to a linear color space to match the linear calculations of your sophisticated lighting.
24.3.4 Two Wrongs Don't Make a Right
The most common gamma mistake made in rendering is using nonlinear color textures for shading and then not applying gamma correction to the final image. This double error is much less noticeable than making just one of these mistakes, because the corrections required for each are roughly opposites. However, this situation creates many problems that can be easily avoided.
Figure 24-4 shows a comparison between two real-time renderings using a realistic skin shader. (For more information on skin shaders, see Chapter 14 of this book, "Advanced Techniques for Realistic Real-Time Skin Rendering.") The left image converted the diffuse color texture into a linear space because the texture came from several JPEG photographs. Lighting (including subsurface scattering) and shading were performed correctly in a linear space and then the final image was gamma-corrected for display on average nonlinear display devices.
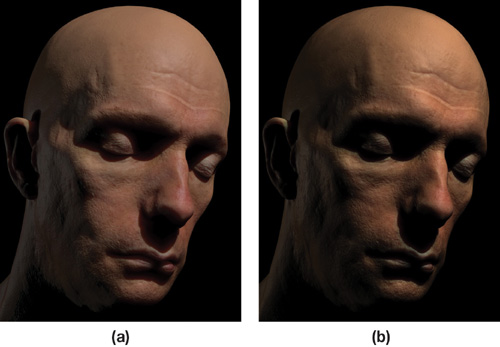
Figure 24-4 Rendering with Proper Gamma Correction () and Rendering Ignoring Gamma ()
The image on the right made neither of these corrections and exhibits several problems. The skin tone from the color photographs is changed because the lighting was performed in a nonlinear space, and as the light brightened and darkened the color values, the colors were inadvertently changed. (The red levels of the skin tones are higher than the green and blue levels and thus receive a different boost when brightened or darkened by light and shadow.) The white specular light, when added to the diffuse lighting, becomes yellow. The shadowed regions become too dark, and the subsurface scattering (particularly the subtle red diffusion into shadowed regions) is almost totally missing because it is squashed by the gamma curve when it's displayed.
Adjusting lighting becomes problematic in a nonlinear space. If we take the same scenes in Figure 24-4 and render them now with the light intensities increased, the problems in the nonlinear version become worse, as you can see in Figure 24-5. As a rule, if color tones change as the same object is brightened or darkened, then most likely nonlinear lighting is taking place and gamma correction is needed.
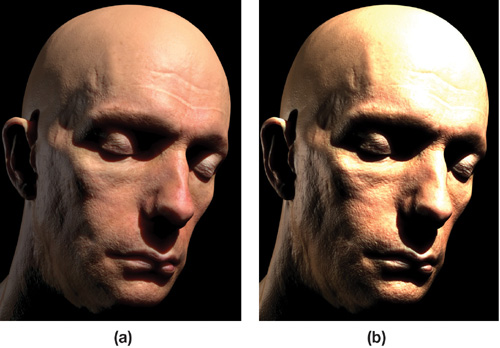
Figure 24-5 Rendering with Proper Gamma Correction () and Rendering Incorrect Gamma ()
A common problem encountered when subsurface scattering is used for skin rendering (when gamma correction is ignored) is the appearance of a blue-green glow around the shadow edges and an overly waxy-looking skin, as shown in Figure 24-6. These problems arise when the scattering parameters are adjusted to give shadow edges the desired amount of red bleeding (as seen in Figure 24-5). This effect is hard to achieve in a nonlinear color space and requires a heavily weighted broad blur of irradiance in the red channel. The result causes far too much diffusion in the bright regions of the face (giving a waxy look) and causes the red to darken too much as it approaches a shadow edge (leaving a blue-green glow).

Figure 24-6 Tweaking Subsurface Scattering When Rendering Without Gamma Correction Is Problematic
24.4 The Cure
Gamma correction is the practice of applying the inverse of the monitor transformation to the image pixels before they're displayed. That is, if we raise pixel values to the power 1/gamma before display, then the display implicitly raising to the power gamma will exactly cancel it out, resulting, overall, in a linear response (see Figure 24-2).
The usual implementation is to have your windowing systems apply color-correction lookup tables (LUTs) that incorporate gamma correction. This adjustment allows all rendering, compositing, or other image manipulation to use linear math and for any linear-scanned images, paintings, or rendered images to be displayed correctly.
Animation and visual effects studios, as well as commercial publishers, are very careful with this process. Often it's the exclusive job of a staff person to understand color management for their monitors, compositing pipeline, film and video scanning, and final outputs. In fact, for high-end applications, simple gamma correction is not enough. Often compositors use a much more sophisticated 3D color LUT derived from careful measurements of the individual displays or film stocks' color-response curves. [4] In contrast to visual effects and animation for film, game developers often get this process wrong, which leads to the artifacts discussed in this chapter. This is one reason why most (but not all) CG for film looks much better than games—a reason that has nothing to do with the polygon counts, shading, or artistic skills of game creators. (It's also sometimes a reason why otherwise well-made film CG looks poor—because the color palettes and gammas have been mismatched by a careless compositor.)
Joe GamePlayer doesn't have a calibrated monitor. We don't know the right LUTs to apply for his display, and in any case, he doesn't want to apply gamma-correcting LUTs to his entire display. Why? Because then the ordinary JPEG files viewed with Web browsers and the like will look washed out and he won't understand why. (Film studios don't care if random images on the Internet look wrong on an artist's workstation, as long as their actual work product—the film itself—looks perfect in the theatre, where they have complete control.) But simple gamma correction for the "average" monitor can get us most of the way there. The remainder of this chapter will present the easiest solutions to improve and avoid these artifacts in games you are developing.
24.4.1 Input Images (Scans, Paintings, and Digital Photos)
Most images you capture with scanning or digital photography are likely already gamma-corrected (especially if they are JPEGs by the time they get to you), and therefore are in a nonlinear color space. (Digital camera JPEGs are usually sharpened by the camera as well for capturing textures; try to use a RAW file format to avoid being surprised.) If you painted textures without using a gamma LUT, those paintings will also be in monitor color space. If an image looks right on your monitor in a Web browser, chances are it has been gamma-corrected and is nonlinear.
Any input textures that are already gamma-corrected need to be brought back to a linear color space before they can be used for shading or compositing. You want to make this adjustment for texture values that are used for (linear) lighting calculations. Color values (such as light intensities and diffuse reflectance colors) should always be uncorrected to a linear space before they're used in shading. Alpha channels, normal maps, displacement values (and so on) are almost certainly already linear and should not be corrected further, nor should any textures that you were careful to paint or capture in a linear fashion.
All modern GPUs support sRGB texture formats. These formats allow binding gamma-corrected pixel data directly as a texture with proper gamma applied by the hardware before the results of texture fetches are used for shading. On NVIDIA GeForce 8-class (and future) hardware, all samples used in a texture filtering operation are linearized before filtering to ensure the proper filtering is performed (older GPUs apply the gamma post-filtering). The correction applied is an IEC standard (IEC 61966-2-1) that corresponds to a gamma of roughly 2.2 and is a safe choice for nonlinear color data where the exact gamma curve is not known. Alpha values, if present, are not corrected.
Appropriate sRGB formats are defined for all 8-bit texture formats (RGB, RGBA, luminance, luminance alpha, and DXT compressed), both in OpenGL and in DirectX. Passing GL_SRGB_EXT instead of GL_RGB to glTexImage2D, for example, ensures that any shader accesses to the specified texture return linear pixel values.
The automatic sRGB corrections are free and are preferred to performing the corrections manually in a shader after each texture access, as shown in Listing 24-1, because each pow instruction is scalar and expanded to two instructions. Also, manual correction happens after filtering, which is incorrectly performed in a nonlinear space. The sRGB formats may also be preferred to preconverting textures to linear versions before they are loaded. Storing linear pixels back into an 8-bit image is effectively a loss of precision in low light levels and can cause banding when the pixels are converted back to monitor space or used in further shading.
Example 24-1. Manually Converting Color Values to a Linear Space
Texture lookups can apply inverse gamma correction so that the rest of your shader is working with linear values. However, using an sRGB texture is faster, allows proper linear texture filtering (GeForce 8 and later), and requires no extra shader code.
float3 diffuseCol =
pow(f3tex2D(diffTex, texCoord),
2.2); // Or (cheaper, but assuming gamma of 2.0 rather than 2.2)
float3 diffuseCol = f3tex2D(diffTex, texCoord);
diffuseCol = diffuseCol * diffuseCol;Managing shaders that need to mix linear and nonlinear inputs can be an ugly logistical chore for the engine programmers and artists who provide textures. The simplest solution, in many cases, is to simply require all textures to be precorrected to linear space before they're delivered for use in rendering.
24.4.2 Output Images (Final Renders)
The last step before display is to gamma-correct the final pixel values so that when they're displayed on a monitor with nonlinear response, the image looks "correct." Specifying an sRGB frame buffer leaves the correction to the GPU, and no changes to shaders are required. Any value returned in the shader is gamma-corrected before storage in the frame buffer (or render-to-texture buffer). Furthermore, on GeForce 8-class and later hardware, if blending is enabled, the previously stored value is converted back to linear before blending and the result of the blend is gamma-corrected. Alpha values are not gamma-corrected when sRGB buffers are enabled. If sRGB buffers are not available, you can use the more costly solution of custom shader code, as shown in Listing 24-2; however, any blending, if enabled, will be computed incorrectly.
Example 24-2. Last-Stage-Output Gamma Correction
If sRGB frame buffers are not available (or if a user-defined gamma value is exposed), the following code will perform gamma correction.
float3 finalCol = do_all_lighting_and_shading();
float pixelAlpha = compute_pixel_alpha();
return float4(
pow(finalCol, 1.0 / 2.2),
pixelAlpha); // Or (cheaper, but assuming gamma of 2.0 rather than 2.2)
return float4(sqrt(finalCol), pixelAlpha);24.4.3 Intermediate Color Buffers
A few subtle points should be kept in mind. If you are doing any kind of post-processing pass on your images, you should be doing the gamma correction as the last step of the last post-processing pass. Don't render, correct, and then do further math on the result as if it were a linear image.
Also, if you are rendering to create a texture, you need to either (a) gamma-correct, and then treat the texture as a nonlinear input when performing any further processing of it, or (b) not gamma-correct, and treat the texture as linear input for any further processing. Intermediate color buffers may lose precision in the darks if stored as 8-bit linear images, compared to the precision they would have as gamma-corrected images. Thus, it may be beneficial to use 16-bit floating-point or sRGB frame-buffer and sRGB texture formats for rendering and accessing intermediate color buffers.
24.5 Conclusion
OpenGL, DirectX, and any shaders you write are probably performing math as if all texture inputs, light/material interactions, and outputs are linear (that is, light intensities sum; diffuse reflectivities multiply). But it is very likely that your texture inputs may be nonlinear, and it's almost certain that your user's uncalibrated and uncorrected monitor applies a nonlinear color-space transformation. This scenario leads to all sorts of artifacts and inaccuracies, some subtle (such as mipmap filtering errors) and some grossly wrong (such as very incorrect light falloff).
We strongly suggest that developers take the following simple steps:
- Assume that most game players are using uncalibrated, uncorrected monitors that can roughly be characterized by an exponential response with gamma = 2.2. (For an even higher-quality end-user experience: Have your game setup display a gamma calibration chart and let the user choose a good gamma value.)
- When performing lookups from nonlinear textures (those that look "right" on uncorrected monitors) that represent light or color values, raise the results to the power gamma to yield a linear value that can be used by your shader. Do not make this adjustment for values already in a linear color space, such as certain high-dynamic-range light maps or images containing normals, bump heights, or other noncolor data. Use sRGB texture formats, if possible, for increased performance and correct texture filtering on GeForce 8 GPUs (and later).
- Apply a gamma correction (that is, raise to power 1/gamma) to the final pixel values as the very last step before displaying them. Use sRGB frame-buffer extensions for efficient automatic gamma correction with proper blending.
Carefully following these steps is crucial to improving the look of your game and especially to increasing the accuracy of any lighting or material calculations you are performing in your shaders.
24.6 Further Reading
In this chapter, we've tried to keep the descriptions and advice simple, with the intent of making a fairly nontechnical argument for why you should use linear color spaces. In the process, we've oversimplified. For those of you who crave the gory details, an excellent treatment of the gamma problem can be found on Charles Poynton's Web page: http://www.poynton.com/GammaFAQ.html.
The Wikipedia entry on gamma correction is surprisingly good:
For details regarding sRGB hardware formats in OpenGL and DirectX, see these resources:
- http://www.nvidia.com/dev_content/nvopenglspecs/GL_EXT_texture_sRGB.txt
- http://www.opengl.org/registry/specs/EXT/framebuffer_sRGB.txt
- http://msdn2.microsoft.com/en-us/library/bb173460.aspx
Thanks to Gary King and Mark Kilgard for their expertise on sRGB and their helpful comments regarding this chapter. Special thanks to actor Doug Jones for kindly allowing us to use his likeness. And finally, Figure 24-2 was highly inspired by a very similar version we found on Wikipedia.
- Contributors
- Foreword
- Part I: Geometry
-
- Chapter 1. Generating Complex Procedural Terrains Using the GPU
- Chapter 2. Animated Crowd Rendering
- Chapter 3. DirectX 10 Blend Shapes: Breaking the Limits
- Chapter 4. Next-Generation SpeedTree Rendering
- Chapter 5. Generic Adaptive Mesh Refinement
- Chapter 6. GPU-Generated Procedural Wind Animations for Trees
- Chapter 7. Point-Based Visualization of Metaballs on a GPU
- Part II: Light and Shadows
-
- Chapter 8. Summed-Area Variance Shadow Maps
- Chapter 9. Interactive Cinematic Relighting with Global Illumination
- Chapter 10. Parallel-Split Shadow Maps on Programmable GPUs
- Chapter 11. Efficient and Robust Shadow Volumes Using Hierarchical Occlusion Culling and Geometry Shaders
- Chapter 12. High-Quality Ambient Occlusion
- Chapter 13. Volumetric Light Scattering as a Post-Process
- Part III: Rendering
-
- Chapter 14. Advanced Techniques for Realistic Real-Time Skin Rendering
- Chapter 15. Playable Universal Capture
- Chapter 16. Vegetation Procedural Animation and Shading in Crysis
- Chapter 17. Robust Multiple Specular Reflections and Refractions
- Chapter 18. Relaxed Cone Stepping for Relief Mapping
- Chapter 19. Deferred Shading in Tabula Rasa
- Chapter 20. GPU-Based Importance Sampling
- Part IV: Image Effects
-
- Chapter 21. True Impostors
- Chapter 22. Baking Normal Maps on the GPU
- Chapter 23. High-Speed, Off-Screen Particles
- Chapter 24. The Importance of Being Linear
- Chapter 25. Rendering Vector Art on the GPU
- Chapter 26. Object Detection by Color: Using the GPU for Real-Time Video Image Processing
- Chapter 27. Motion Blur as a Post-Processing Effect
- Chapter 28. Practical Post-Process Depth of Field
- Part V: Physics Simulation
-
- Chapter 29. Real-Time Rigid Body Simulation on GPUs
- Chapter 30. Real-Time Simulation and Rendering of 3D Fluids
- Chapter 31. Fast N-Body Simulation with CUDA
- Chapter 32. Broad-Phase Collision Detection with CUDA
- Chapter 33. LCP Algorithms for Collision Detection Using CUDA
- Chapter 34. Signed Distance Fields Using Single-Pass GPU Scan Conversion of Tetrahedra
- Chapter 35. Fast Virus Signature Matching on the GPU
- Part VI: GPU Computing
-
- Chapter 36. AES Encryption and Decryption on the GPU
- Chapter 37. Efficient Random Number Generation and Application Using CUDA
- Chapter 38. Imaging Earth's Subsurface Using CUDA
- Chapter 39. Parallel Prefix Sum (Scan) with CUDA
- Chapter 40. Incremental Computation of the Gaussian
- Chapter 41. Using the Geometry Shader for Compact and Variable-Length GPU Feedback
- Preface