
GPU Gems 3
GPU Gems 3 is now available for free online!
The CD content, including demos and content, is available on the web and for download.
You can also subscribe to our Developer News Feed to get notifications of new material on the site.
Chapter 36. AES Encryption and Decryption on the GPU
Takeshi Yamanouchi
SEGA Corporation
In this chapter, we take up integer stream processing on the GPU, which has been at best a difficult task to do on the GPU up to now.
Traditionally the GPU has been used almost exclusively for floating-point operations, because integer operations could only be done using the mantissa of floats; thus, processes that required bitwise logical operations were impossible. Another issue was that we had to render the output of the GPU to textures or pixel buffers before we could get to our results. Therefore, to process streaming data, we needed to write tricky graphics code.
However, with the advent of the new GeForce 8 Series GPU, several new extensions and functions have been introduced to GPU programming. First, the new integerprocessing features include not only the arithmetic operations but also the bitwise logical operations (such as AND and OR) and the right/left shift operations. Second, array parameters and the new texture-buffer object provide a flexible way of referring to integer-indexed tables. And finally, with the new "transform feedback mode," it is now possible to store our results without the need to render to textures or pixel buffers.
In this chapter we present an application of these new features by implementing Advanced Encryption Standard (AES) (NIST 2001) encryption and decryption on the GPU. Unlike previous attempts (Cook et al. 2005) and precisely thanks to these new features, our implementation shows slight performance gains over CPU implementations.
In addition, within the AES system, we consider several block-cipher modes of operation (Dworkin 2001) that demonstrate the practical cases where the GPU can be used to optimize performance through parallel processing, and other cases where it cannot.
36.1 New Functions for Integer Stream Processing
For our implementation of the AES encryption system, we use the new OpenGL extensions provided by NVIDIA in the GeForce 8 Series (NVIDIA 2006, OpenGL.org 2007). In this section we briefly introduce some of these extensions.
36.1.1 Transform Feedback Mode
Transform feedback mode is a new OpenGL mode of operation. In this mode the GPU can send its output to a buffer before the rasterization stage. This way we can store the output of the shaders into buffer objects as vertex attributes. Figure 36-1 illustrates the process.
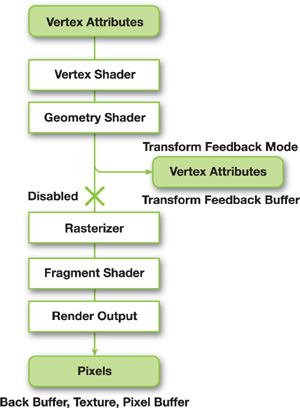
Figure 36-1 The Transform Feedback Mode Processing Pipeline
Rendering in transform feedback mode is like regular rendering from buffer objects except for the following differences:
- The GL's target parameter is changed to GL_TRANSFORM_FEEDBACK_BUFFER_NV.
- We need to specify the output attributes and whether each of them is output into a separate buffer object or they are all output interleaved into a single buffer object.
- The output buffer must be bound through special new API calls such as glBindBufferRangeNV(), and so on.
- Primitive draw calls have to be enclosed between glBeginTransformFeedbackNV() and glEndTransformFeedbackNV() calls in a similar fashion to glBeginQuery() and glEndQuery().
- Rasterization can also be optionally disabled, as we do in this chapter, because we do not need any other subsequent pipeline stages. This is done through the following call: glEnable(GL_RASTERIZER_DISCARD_NV).
36.1.2 GPU Program Extensions
We use two of the new features introduced in the assembly instruction set.
First, when declaring a register, we can either specify its type, such as FLOAT or INT, or just leave it typeless. We can also specify a type for each executed instruction that declares how the instruction should interpret its operands. This is done by using the type indicators following the opcodes. These type indicators are .F for float, .S for signed int, and .U for unsigned int:
TEMP r0, r1, r2; // typeless registers
MOV.U r0, 0x3f800000; // r0 = 1.0f
MAD.F r1, r0, 2, -1; // r1 = 1.0f
MAD.S r2, r0, 2, -1; // r2 = 0x7effffffSecond, we can refer to tables using an integer index, array parameters, or one of the newly introduced texture-buffer objects.
INT TEMP r0, r1;
MOV.S r0.x, 10;
MOV.S r0, 0; // integer index
MOV.S r1.x, table[r0.x].x; // array parameter
TXF.S r1.x, r0.x, texture[1], BUFFER; // texture-buffer objectOn current GeForce 8 Series GPUs, the texture-buffer-object approach generally yields better performance than using array parameters.
36.2 An Overview of the AES Algorithm
The AES algorithm is currently the standard block-cipher algorithm that has replaced the Data Encryption Standard (DES). Back in 1997 the National Institute of Standards and Technology (NIST) made a public call for new cipher algorithms that could replace the DES. A rough summary of the requirements made by NIST for the new AES were the following:
- Symmetric-key cipher
- Block cipher
- Support for 128-bit block sizes
- Support for 128-, 192-, and 256-bit key lengths
Finally in October 2000, the Rijndael algorithm was chosen as the basis for the new standard encryption algorithm (Hironobu 2001). The original Rijndael algorithm also supported both fixed-size and variable-size bit cipher blocks. However, currently the Federal Information Processing Standards specification for the AES algorithm supports only the fixed-size, 128-bit blocks.
The operation of the AES algorithm is shown in Figure 36-2. The encryption step uses a key that converts the data into an unreadable ciphertext, and then the decryption step uses the same key to convert the ciphertext back into the original data. This type of key is a symmetric key; other algorithms require a different key for encryption and decryption.
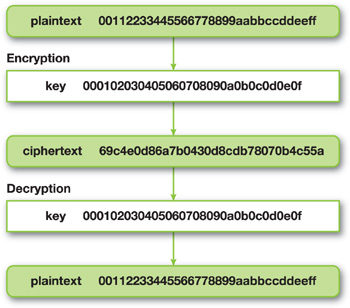
Figure 36-2 AES Cipher Operation
The precise steps involved in the algorithm can be seen in Figure 36-3. The process is relatively simple, but some brief cryptographic explanations are necessary to understand what is going on. In cryptography, algorithms such as AES are called product ciphers. For this class of ciphers, encryption is done in rounds, where each round's processing is accomplished using the same logic. Moreover, many of these product ciphers, including AES, change the cipher key at each round. Each of these round keys is determined by a key schedule, which is generated from the cipher key given by the user.
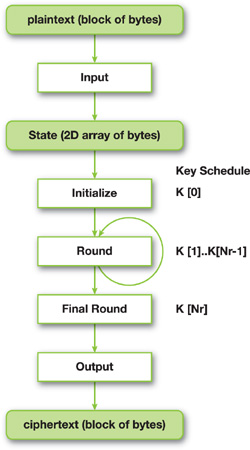
Figure 36-3 An Illustration of the AES Algorithm
Generally speaking, the strength of an encryption by product ciphers can be heightened by increasing the number of rounds used to process the data. The AES standard specifies that the number of rounds is determined by the length of the cipher key, as shown in Figure 36-4.
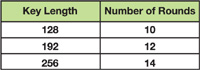
Figure 36-4 Key Length and the Number of Rounds
36.3 The AES Implementation on the GPU
Now that we know what the AES algorithm is supposed to do, let's see what its implementation looks like as a vertex program. The code given throughout this chapter uses C-style macros and comments to improve readability of the assembly language. These—like those in the ROT8 macro shown in Listing 36-1—get filtered out using the standard C preprocessor.
Example 36-1. Head of the AES Cipher Vertex Program
!!NVvp4.0
/*
* aes.vpt -- AES encryption and decryption
* Author Yamanouchi_Takeshi@sega.co.jp
*/
// input, output
ATTRIB state_in = vertex.attrib[0];
OUTPUT state_out = result.texcoord[0];
// macros
INT TEMP _tmp0, _tmp1; // macro work
#define ROT8(_arg) \
SHL.U _tmp0, _arg, 8; \
SHR.U _arg, _arg, 24; \
OR _arg, _arg, _tmp0In this application we expand the cipher key using the CPU and store the key schedule in the GPU program-local parameters. Besides the key schedule, other arguments and tables can also be stored directly in advance to improve performance, as shown in Listing 36-2.
Example 36-2. Program Parameters for Arguments and Constant Tables
// parameters
// cipher mode, 0:encrypt, 1:decrypt
INT PARAM mode = program.local[MODE];
// number of rounds
INT PARAM num_round = program.local[NUM_ROUND];
// key schedule for encryption
INT PARAM enc_key[15] = { program.local[ENC_KEY_BEGIN..ENC_KEY_END] };
// key schedule for decryption
INT PARAM dec_key[15] = { program.local[DEC_KEY_BEGIN..DEC_KEY_END] };36.3.1 Input/Output and the State
AES encryption operates over a two-dimensional array of bytes, called the state. During the input step, we slice our data into sequential blocks of 16 bytes and unpack it into 4x4 arrays that we push onto the GPU's registers. Finally, during the output step, we pack these 4x4 arrays back into sequential blocks of 16 bytes and stream the results back to the transform feedback buffer, as shown in Figure 36-5.
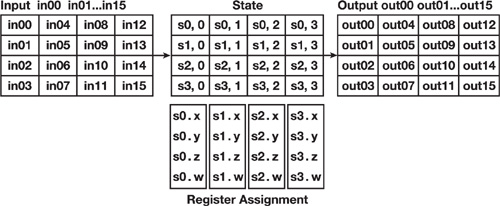
Figure 36-5 Input, State, Output, and Register Assignment for the Streamed Data
The code fragments in Listing 36-3 go into the details for these steps. First we define our packing and unpacking methods as macros. Then we have an unpack_state_in: subroutine, which unpacks the input into the current state matrix, and a pack_state_out: subroutine, which packs the current state matrix back to the output stream.
The registers for state_in and state_out consist of four components of 32-bit integers each, giving us the standard AES block size of 128 bits for processing.
Example 36-3. The State and Input (Unpack)/Output (Pack) Subroutine
// registers
INT TEMP s0, s1, s2, s3; // state
#define UNPACK(_res, _arg) \
SHR _res.w, _arg, 24; \
SHR _res.z, _arg, 16; \
SHR _res.y, _arg, 8; \
MOV.U _res.x, _arg; \
AND _res, _res, 0xff
#define PACK(_res, _arg) \
SHL _tmp0.w, _arg.w, 24; \
SHL _tmp0.z, _arg.z, 16; \
SHL _tmp0.y, _arg.y, 8; \
OR _tmp0.w, _tmp0.w, _tmp0.z; \
OR _tmp0.w, _tmp0.w, _tmp0.y; \
OR _res, _tmp0.w, _arg.x
unpack_state_in:
// arg0: round key
XOR tmp, state_in, arg0;
UNPACK(s0, tmp.x);
UNPACK(s1, tmp.y);
UNPACK(s2, tmp.z);
UNPACK(s3, tmp.w);
RET;
pack_state_out:
// arg0: round key
PACK(tmp.x, s0);
PACK(tmp.y, s1);
PACK(tmp.z, s2);
PACK(tmp.w, s3);
XOR state_out, tmp, arg0;
RET;36.3.2 Initialization
During the initialization stage, we do an AddRoundKey operation, which is an XOR operation on the state by the round key, as determined by the key schedule. In our case, we perform unpacking and round key addition together in the unpack_state_in: subroutine.
36.3.3 Rounds
A round for the AES algorithm consists of four operations: the SubBytes operation, the ShiftRows operation, the MixColumns operation, and the previously mentioned AddRoundKey operation.
The SubBytes Operation
The SubBytes operation substitutes bytes independently, in a black-box fashion, using a nonlinear substitution table called the S-box, as shown in Figure 36-6.
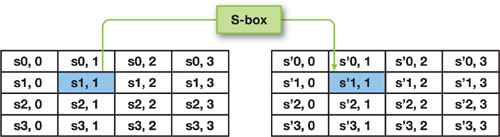
Figure 36-6 The SubBytes Operation
The S-box is a uniform table calculated in advance and stored into the texture-buffer objects as texture[] (see the code in Listing 36-2). In our implementation we store the encryption table in texture[1] and the transformation table used for decryption in texture[2], as you can see in Listing 36-4.
Example 36-4. SubBytes for the First Row of the State
sub_bytes_shift_rows:
// first row
TXF.U s0.x, s0.x, texture[1], BUFFER; // texture[1]: s_box
TXF.U s1.x, s1.x, texture[1], BUFFER;
TXF.U s2.x, s2.x, texture[1], BUFFER;
TXF.U s3.x, s3.x, texture[1], BUFFER;The ShiftRows Operation
The ShiftRows operation shifts the last three rows of the state cyclically, effectively scrambling row data, as shown in Figure 36-7.
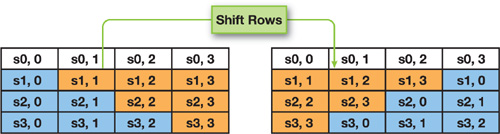
Figure 36-7 The ShiftRows Operation
One simple optimization we can do is to combine the SubBytes and ShiftRows operations into a single subroutine that we call sub_bytes_shift_rows:. The continuation of the code from the previous section that combines both operations as one is shown in Listing 36-5.
Example 36-5. SubBytes and ShiftRows for the Second, Third, and Fourth Rows
// second row
TXF.U tmp, s0.y, texture[1], BUFFER;
TXF.U s0.y, s1.y, texture[1], BUFFER;
TXF.U s1.y, s2.y, texture[1], BUFFER;
TXF.U s2.y, s3.y, texture[1], BUFFER;
MOV.U s3.y, tmp;
// third row
TXF.U tmp, s0.z, texture[1], BUFFER;
TXF.U s0.z, s2.z, texture[1], BUFFER;
MOV.U s2.z, tmp;
TXF.U tmp, s1.z, texture[1], BUFFER;
TXF.U s1.z, s3.z, texture[1], BUFFER;
MOV.U s3.z, tmp;
// fourth row
TXF.U tmp, s3.w, texture[1], BUFFER;
TXF.U s3.w, s2.w, texture[1], BUFFER;
TXF.U s2.w, s1.w, texture[1], BUFFER;
TXF.U s1.w, s0.w, texture[1], BUFFER;
MOV.U s0.w, tmp;
RET;The MixColumns Operation
The next step is the MixColumns operation, which has the purpose of scrambling the data of each column. This operation is done by performing a matrix multiplication upon each column vector, as shown in Figure 36-8.
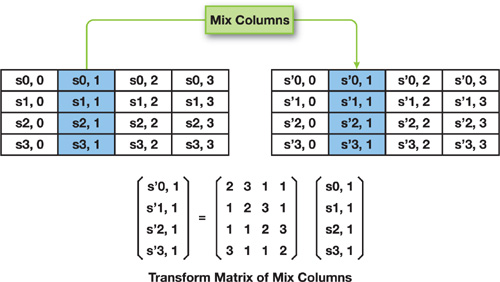
Figure 36-8 The MixColumns Operation
Because the multiplication is over a finite field of the AES, we cannot use the usual MUL operation. The closure of the finite field is within a byte range. So we store the results of the multiplication by (0x2, 0x1, 0x1, 0x3) in texture[3]. The resulting bytes are packed into a 32-bit integer in little-endian form, such as 0x03010102.
The resulting transformation matrix is shifted by columns; therefore, the results are rotated by the ROT8(). . ROT24() macros. Finally, we add them together by XOR'ing and unpacking into the state, as seen in Listing 36-6.
Example 36-6. MixColumns and AddRoundKey
mix_columns_add_round_key:
// arg0: round key
TXF.U mix0.x, s0.x, texture[3], BUFFER; // texture[3]: mix_col
TXF.U mix0.y, s1.x, texture[3], BUFFER;
TXF.U mix0.z, s2.x, texture[3], BUFFER;
TXF.U mix0.w, s3.x, texture[3], BUFFER;
TXF.U mix1.x, s0.y, texture[3], BUFFER;
. . .
TXF.U mix3.w, s3.w, texture[3], BUFFER;
ROT8(mix1);
ROT16(mix2);
ROT24(mix3);
XOR tmp, arg0, mix0; // add round key
XOR tmp, tmp, mix1;
XOR tmp, tmp, mix2;
XOR tmp, tmp, mix3;
UNPACK(s0, tmp.x);
UNPACK(s1, tmp.y);
UNPACK(s2, tmp.z);
UNPACK(s3, tmp.w);
RET;During decryption, the multiplication results are stored in texture[4]. The coefficients are (0xe, 0x9, 0xd, 0xb).
In brief, all components of texture[] at this point are as follows:
- texture[1] holds the encryption S-box data.
- texture[2] holds the decryption S-box data.
- texture[3] holds the encryption MixColumns data.
- texture[4] holds the decryption MixColumns data.
The AddRoundKey Operation
This operation determines the current round key from the key schedule, where the register arg0 serves as the argument. As an optimization we can also combine the MixColumns and AddRoundKey operations into a single subroutine named mix_columns_add_round_key:.
The code in Listing 36-7 is the encryption loop. Note that the cost of control flow operations has significantly decreased in the GeForce 8 Series: so much so that unrolling the loop—which would have further complicated the code—is unnecessary to obtain good performance.
Example 36-7. AES Encryption Loop
encrypt:
// input & first round
MOV.U arg0, enc_key[0];
CAL unpack_state_in;
// loop round
SUB.S cnt.x, num_round.x, 1;
MOV.S cnt.y, 1;
REP.S cnt.x;
CAL sub_bytes_shift_rows;
MOV.U arg0, enc_key[cnt.y];
CAL mix_columns_add_round_key;
ADD.S cnt.y, cnt.y, 1;
ENDREP;
// final round & output
CAL sub_bytes_shift_rows;
MOV.U arg0, enc_key[cnt.y];
CAL pack_state_out;
RET;36.3.4 The Final Round
The final round has no MixColumns operation. The AddRoundKey operation is combined with packing into a single subroutine called pack_state_out: in a similar fashion to what we did for initialization.
36.4 Performance
Now that we have a working AES implementation, let us measure the performance of GPU-based encryption. The decryption is omitted because it performs the same as the encryption in the AES algorithm. Our tests were performed on a test machine with the following specifications:
- CPU: Pentium 4, 3 GHz, 2 MB Level 2 cache
- Memory: 1 GB
- Video: GeForce 8800 GTS 640 MB
- System: Linux 2.6, Driver 97.46
36.4.1 Vertex Program vs. Fragment Program
We compared the performance of the vertex program in the transform feedback mode pipeline with that of the fragment program in the traditional rendering pipeline. The fragment program is the same code as the vertex program except that input/output registers were redefined appropriately, exploiting the GPU's unified architecture.
Our results were obtained by processing a plaintext of 128 MB filled with random numbers and averaging measurements from ten runs. As illustrated in Figure 36-9, the throughput for the vertex program is 53 MB/sec, whereas for the fragment program, the throughput is 95 MB/sec with a batch size of 1 MB. Our implementation spends most of its processing time in referencing tables—in other words, fetching textures.
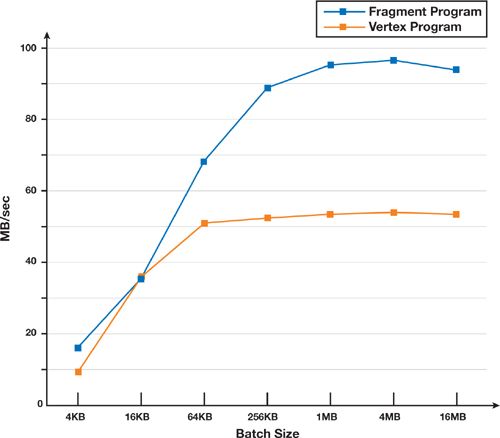
Figure 36-9 Vertex Program vs. Fragment Program
36.4.2 Comparison to CPU-Based Encryption
The openssl command has benchmarks for determining the speed of their cipher algorithms on the CPU. We measured the speed of these CPU-based encryptions on the same test machine, and we got results of about 55 MB/sec using the same AES algorithm. Compared to the speed of the CPU-based implementations, our GPU-based encryption is thus almost the same speed for the vertex program, and about 1.7 times faster for the fragment program. The transform feedback mode makes it easy to write code for data streaming, but it does not perform as well for now.
36.5 Considerations for Parallelism
There are some considerations to be made based on the mode of operation for our block ciphers that affect suitability for parallelism. In this section, we look at a few different modes and how they may affect suitability for parallel processing.
36.5.1 Block-Cipher Modes of Operation
Electronic Code Book Mode
The encrypting operation of each block is called the electronic code book (ECB) mode. In ECB encryption, each block is operated upon independently, as shown in Figure 36-10.
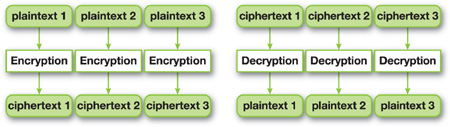
Figure 36-10 ECB Mode Encryption and Decryption
This mode of operation makes it possible to compute ciphertexts in parallel, and it was the mode of operation used for all the tests in Section 36.4.
In ECB mode, the same bit blocks will always generate the same ciphertext. But although the ciphertext is not directly readable, there is a possibility that the content can be guessed based on the resulting pattern. Figure 36-11 shows a 256x256 texture encrypted in ECB mode, and although it cannot be directly read, there is an evident pattern in the cipher texture.

Figure 36-11 Plain Texture and Cipher Texture in ECB Mode
Cipher-Block Chaining Mode
The cipher-block chaining (CBC) mode overcomes the ECB mode's weakness by chaining each cipher into the next block. This is done by chaining (XOR'ing) our current plaintext block with the previously encrypted block. The first block has no previous block, so we use an initial vector (IV) instead that is passed during initialization along with the symmetric key for decryption. See Figure 36-12.
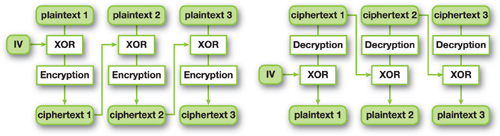
Figure 36-12 CBC Mode Encryption and Decryption
In CBC mode, because plaintexts are scrambled before encryption, the ciphertext pattern never appears in the final result. So we cannot see the "AES" letters in Figure 36-13 as we could in Figure 36-11.

Figure 36-13 The Cipher Texture in CBC Mode
However, because CBC mode needs the ciphertexts of each previous step to process the next step, it is not possible to begin the encryption of a block until its previous block has been encrypted. So we can't hope for parallel processing during the encryption stage of this mode.
36.5.2 Modes for Parallel Processing
Decryption in CBC Mode
As we just mentioned, in CBC mode, encryption cannot be processed in parallel because it requires the results of each previous step. However, fortunately we can decrypt our results using parallel processing. This is because after encryption, we already know the states of all the previous ciphertext blocks and the IV needed for decryption.
The gain to be obtained here is that we often need to do more decryption than encryption, and many times decryption is required to have higher throughput speeds, such as when preprocessing and storing cipher textures encrypted in CBC mode into distribution files; these files can then be decrypted in parallel during loading without any noticeable delays.
Counter Mode
Nevertheless, there are cases when fast encryption is highly desirable, such as for secure communications, where the parallel processing of the encryption stage would greatly speed up the overall performance. In these cases, counter (CTR) mode can be used. The CTR algorithm's procedure is shown in Figure 36-14. First, we make the input block by indexing the current block, called a counter block. We then encrypt it using the symmetric key, and XOR'ing with the original plaintext block.
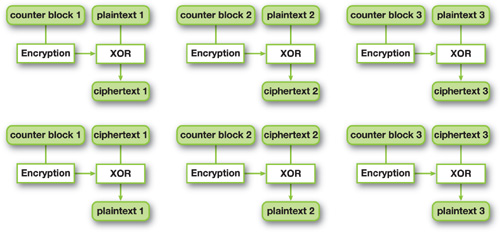
Figure 36-14 CTR Mode Encryption and Decryption
The decryption for CTR can be done following the same steps. Thus we can encrypt and decrypt each cipher block independently, giving us the benefit of true parallelization.
36.6 Conclusion and Future Work
Thanks to new capabilities added to the GPU, we can now truly perform integer stream processing. As a showcase, we presented an implementation for an AES system that relies heavily on integer processing.
Our implementation is OpenGL-based, but another way to program the latest generation of NVIDIA GPUs is to use CUDA (NVIDIA 2007). As future work, we plan to implement the same algorithm using CUDA and compare performance against the OpenGL implementation.
Another direction of future work is to find other novel areas besides AES encryption that could benefit from GPU parallel processing power.
36.7 References
Cook, Debra L., John Ioannidis, Angelos D. Keromytis, and Jake Luck. 2005. "CryptoGraphics: Secret Key Cryptography Using Graphics Cards." In RSA Conference, Cryptographer's Track (CT-RSA), pp. 334–350.
Dworkin, M. 2001. "Recommendation for Block Cipher Modes of Operation: Methods and Techniques." NIST Special Publication 800-38A. Available online at http://csrc.nist.gov/publications/nistpubs/800-38a/sp800-38a.pdf.
Hironobu, Suzuki. 2001. "Memorandum of DES and AES." Available online (in Japanese only) at http://h2np.net/hironobu/docs/DES_and_AES.pdf.
NIST. 2001. "Advanced Encryption Standard (AES)." FIPS Publication 197. Available online at http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf.
NVIDIA Corporation. 2006. "NVIDIA OpenGL Extension Specifications for the GeForce 8 Series Architecture (G8x)." Available online at http://developer.download.nvidia.com/opengl/specs/g80specs.pdf.
NVIDIA Corporation. 2007. "NVIDIA Compute Unified Device Architecture." http://developer.nvidia.com/cuda/.
OpenGL.org. 2007. "OpenGL Extension Registry." http://www.opengl.org/registry/.
- Contributors
- Foreword
- Part I: Geometry
-
- Chapter 1. Generating Complex Procedural Terrains Using the GPU
- Chapter 2. Animated Crowd Rendering
- Chapter 3. DirectX 10 Blend Shapes: Breaking the Limits
- Chapter 4. Next-Generation SpeedTree Rendering
- Chapter 5. Generic Adaptive Mesh Refinement
- Chapter 6. GPU-Generated Procedural Wind Animations for Trees
- Chapter 7. Point-Based Visualization of Metaballs on a GPU
- Part II: Light and Shadows
-
- Chapter 8. Summed-Area Variance Shadow Maps
- Chapter 9. Interactive Cinematic Relighting with Global Illumination
- Chapter 10. Parallel-Split Shadow Maps on Programmable GPUs
- Chapter 11. Efficient and Robust Shadow Volumes Using Hierarchical Occlusion Culling and Geometry Shaders
- Chapter 12. High-Quality Ambient Occlusion
- Chapter 13. Volumetric Light Scattering as a Post-Process
- Part III: Rendering
-
- Chapter 14. Advanced Techniques for Realistic Real-Time Skin Rendering
- Chapter 15. Playable Universal Capture
- Chapter 16. Vegetation Procedural Animation and Shading in Crysis
- Chapter 17. Robust Multiple Specular Reflections and Refractions
- Chapter 18. Relaxed Cone Stepping for Relief Mapping
- Chapter 19. Deferred Shading in Tabula Rasa
- Chapter 20. GPU-Based Importance Sampling
- Part IV: Image Effects
-
- Chapter 21. True Impostors
- Chapter 22. Baking Normal Maps on the GPU
- Chapter 23. High-Speed, Off-Screen Particles
- Chapter 24. The Importance of Being Linear
- Chapter 25. Rendering Vector Art on the GPU
- Chapter 26. Object Detection by Color: Using the GPU for Real-Time Video Image Processing
- Chapter 27. Motion Blur as a Post-Processing Effect
- Chapter 28. Practical Post-Process Depth of Field
- Part V: Physics Simulation
-
- Chapter 29. Real-Time Rigid Body Simulation on GPUs
- Chapter 30. Real-Time Simulation and Rendering of 3D Fluids
- Chapter 31. Fast N-Body Simulation with CUDA
- Chapter 32. Broad-Phase Collision Detection with CUDA
- Chapter 33. LCP Algorithms for Collision Detection Using CUDA
- Chapter 34. Signed Distance Fields Using Single-Pass GPU Scan Conversion of Tetrahedra
- Chapter 35. Fast Virus Signature Matching on the GPU
- Part VI: GPU Computing
-
- Chapter 36. AES Encryption and Decryption on the GPU
- Chapter 37. Efficient Random Number Generation and Application Using CUDA
- Chapter 38. Imaging Earth's Subsurface Using CUDA
- Chapter 39. Parallel Prefix Sum (Scan) with CUDA
- Chapter 40. Incremental Computation of the Gaussian
- Chapter 41. Using the Geometry Shader for Compact and Variable-Length GPU Feedback
- Preface